Direct Proof that $1 + 3 + 5 + \cdots+ (2n - 1) = n\cdot n$

Question

Prove that for all integers $n$, $n \geq 1$, $$1 + 3 + 5 + \cdots + (2n - 1) = n\cdot n$$

How would I go about proving this?

Answer 1

Hint: When $n=5$, $$\boldsymbol{1+{\color{red}3}+{\color{green}5}+{\color{purple}7}+{\color{blue}9}=} $$ $$\begin{array}{ccccc} \blacksquare & {\color{red}\blacksquare} & {\color{green}\blacksquare} & {\color{purple}\blacksquare} & {\color{blue}\blacksquare}\\ {\color{red}\blacksquare} & {\color{red}\blacksquare} & {\color{green}\blacksquare} & {\color{purple}\blacksquare} & {\color{blue}\blacksquare}\\ {\color{green}\blacksquare} & {\color{green}\blacksquare} & {\color{green}\blacksquare} & {\color{purple}\blacksquare} & {\color{blue}\blacksquare}\\ {\color{purple}\blacksquare} & {\color{purple}\blacksquare} & {\color{purple}\blacksquare} & {\color{purple}\blacksquare} & {\color{blue}\blacksquare}\\ {\color{blue}\blacksquare} & {\color{blue}\blacksquare} & {\color{blue}\blacksquare} & {\color{blue}\blacksquare} & {\color{blue}\blacksquare} \end{array} $$

$$\boldsymbol{=5^2}.$$

Turn this into a general proof.

Answer 2

(1) Proof using the "method of gauss":

$$\begin{eqnarray*} 2(1 + 3+ 5 + \ldots (2n-1)) &=&\big[ 1 + (2n-1)\big] + \big[3 + (2n-3)\big] + \ldots + \big[ (2n-1) + 1\big] \\ &=& \underbrace{2n + 2n + \ldots + 2n}_{\text{$n$ times}} \\ &= &2n(n). \end{eqnarray*}$$ Therefore it follows that $(1 + 3 + \ldots (2n-1)) = n\times n.$

(2) Proof by induction: Let $P(n)$ be the statement:

"For all positive integers $n$, $1 + 3 + \ldots + (2n-1) = n^2$."

For $n=1$ clearly $(2 \cdot 1) - 1 = 1\cdot 1$ so that $P(1)$ is true. So suppose the result holds for $n=k$, i.e. $P(k)$ is true. Since $P(k)$ is true, this means that we have the following equality when $n=k$:

$$1+ 3 + \ldots + (2k-1) = k^2.$$

If you add $2k+1$ to both sides of this equation, you get that

$$ \begin{eqnarray*} 1+ 3 + \ldots +(2k-1) + (2k+1) &=& k\cdot k + (2k+1) \\ &=& k^2 + 2k + 1 \\ &=& (k+1)(k+1) \end{eqnarray*}$$

showing that the result holds for $n=k+1$, i.e. $P(k+1)$ is true. Therefore by the Principle of Mathematical Induction, $1 + 3 + \ldots + (2n-1) = n\cdot n$ for all positive integers $n$.

(3) Suppose you only knew that the sum of $n$ consecutive integers is $n(n+1)/2$. Then

$$\begin{eqnarray*}1 +2 + \ldots + 2n &=& \frac{2n(2n+1)}{2}\\ \implies 1 + 3 + \ldots + (2n-1) &=& n(2n+1) - 2(1 + \ldots + n) \\ &=& 2n^2 + n - 2\left(\frac{n(n+1)}{2}\right) \\ &=& 2n^2 + n - n^2 - n \\ &=& n^2. \end{eqnarray*}$$

(4) Proof using telescoping sums (idea by Bill Dubuque):

$$\begin{eqnarray*} \sum_{k=1}^n 2k-1 &=& \sum_{k=1}^n k^2 - (k-1)^2 \\ &=& (1 - 0) + (2^2 -1 ) + \ldots + n^2 - (n-1)^ 2\\ &=& 1 + (-1 + 2^2) + (-2^2 + 3^2) + \ldots + (-(n-2)^2 + (n-1)^2) + (-(n-1)^2 + n^2)) \\ &=& n^2. \end{eqnarray*}$$

(5) Proof by method of differences (brute force): Let $a_n = \sum_{k=1}^n 2k-1$. Then we see that $a_1 =1 $, $a_2 = 4$, $a_3 = 9$, etc.

Now we look at the first differences $4 - 1 = 3$, $9- 4 = 5$, $16 - 9 = 7$, etc. Then when we look at the second difference, notice that it is constant: $5-3 = 2$, $7- 5= 2$, etc so we conjecture that

$$\sum_{k=1}^n 2k - 1 = an^2 + bn + c$$

where $a,b,c$ are constants to be determined. Plugging in $n = 1,2,3$ gives us a $3 \times 3$ linear system to solve, namely the linear system

$$\left[\begin{array}{ccc} 1 & 1 & 1 \\ 4 & 2 & 1 \\ 9 & 3 & 1 \end{array}\right]\left[\begin{array}{c} a \\ b \\ c \end{array}\right] = \left[\begin{array}{c} 1 \\ 4 \\ 9 \end{array}\right].$$

The determinant of the coefficient matrix is

$$\begin{eqnarray*} 1(2-3) - 1(4-9) + 1(12 - 81) &=& -1 + 5 - 69 \\ &\neq& 0 \end{eqnarray*}$$ so we have a unique solution. It is easy to see that $a = 1, b= 0, c=0$ is a solution to the linear system above. By the previous line, it is the only solution so we are done.

(6) Proof by a direct bash: Suppose you only knew that the sum of the first $n$ integers is $n(n+1)/2$. Then

$$\begin{eqnarray*} \sum_{k=1}^n 2k - 1 &=& \bigg(2\sum_{k=1}^n k \bigg) - \sum_{k=1}^n 1 \\ &=& 2\left(\frac{n(n+1)}{2}\right) - n\\ &=& n^2 + n -n\\ &=& n^2 \end{eqnarray*}.$$

Answer 3

The method of Gauss, graphically:

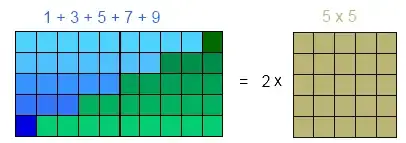
BTW: this corresponds to proof 1 in Benjamin's answer; and the graphic of Eric's answer corresponds to proof 4 (telescoping squares).

Answer 4

Proof that $n^2=1+3+5+\ldots+(2n-1)$ by subdividing the square of side $2n+1$ in two different ways:

Answer 5

$$\begin{eqnarray*} (1 + 3 + 5 + ... + (2n - 1)) &=& (1 + 2 + 3 + ... + 2n) - (2 + 4 + ... + 2n)\\ &=& \sum_{i=1}^{2n}{i} - 2\sum_{i=1}^{n}{i}\\ &=& \frac{(2n)(2n+1)}{2} - 2\left(\frac{n(n+1)}{2}\right)\\ &=& n(2n+1) - n(n+1)\\ &=& n(2n + 1 - n - 1) = n^{2}\end{eqnarray*}$$

Answer 6

Consider this as the sum of a finite recursive series. Each element in the series is calculated from a fixed point a₁=1 by adding 2 to the previous element. So, the equation for any arbitrary a_n is

$$a_{n} = [a_{n-1} + 2, a_{1} = 1] = 1 + 2(n-1)$$

The sum of n terms of this recursive series breaks down to:

$$\sum_{x=1}^{n}[ a_{x-1}+2, a_{1}=1] = 1 + (1 + 2) + ((1 + 2) + 2) + (((1 + 2) + 2) + 2) + \cdot\cdot\cdot + (1 + 2(n-1))$$

By inspection, we see that 1 occurs n times, once per term, and 2 occurs in a triangular fashion (each term contains one more 2 than the previous term). So, this condenses to the quantity of n plus double the (n-1)th triangular number (as the first term has zero 2s):

$$ \sum_{x=1}^{n}( a_{x-1}+2, a_{1}=1) = n + 2\frac{n(n-1)}{2} $$ $$ = n(n-1) + n $$ $$ = n^2 - n + n $$ $$ = n^2$$

QED.

Answer 7

By inspection note that $1 = 1 \cdot 1$, that $1 + 3 = 2 \cdot 2$, and that $1 + 3 + 5 = 3 \cdot 3$.

Next, witness that the difference between any two successive perfect squares $(n - 1)^2$ and $n^2$ is a particular odd integer:

$n^2 - (n - 1)^2 \implies n^2 - (n^2 - 2n + 1) \implies 2n - 1$

Note that this is the very formula which you are summing to generate your series.

So for instance the difference between $3 \cdot 3$ and $2 \cdot 2$ is $2 \cdot 3 - 1 = 5$, corresponding to the $5$ in $3\cdot3 = 1 + 3 + 5$.

If the sum of the series generated so far is a square (shown by inspection), and the next term is from the series generated by $2n - 1$, then after this term is added, the sum must be the next square because the each term obeys the formula for the difference between two successive squares.

Answer 8

Note that $(n+1)^2=n^2+2n+1$. This defines a recursive relationship between $n+1$ and $n$. This means that we can write the function $f(x)=x^2$ recursively as: $f(x)=f(x-1)+2x-1$ with $f(1)=1$. Now, simply expand out $f(x)$ to obtain $f(n)=\sum_{k=1}^{n}2x-1=n^2$.

Answer 9

A nice version of the inductive step is the following:

Using induction, the problem comes down to establishing the result that

$$ n^2=(n-1)^2+(2n-1) $$

Now it is easy to establish this by multiplying out the brackets, but I want to show you another way that I thought of one day. As an example, let $n-1=5$. Then:

\begin{align} 5^2+5 &= 5\times5+5=6\times5\\ 6\times5+6&=6\times6 \end{align}

So $6^2=5^2+5+6$. In general:

\begin{align} (n-1)^2+(n-1)&=(n-1+1)(n-1)=n(n-1)\\ n(n-1)+n&=n(n-1+1)=n^2 \end{align}

So $n^2=(n-1)^2+(n-1)+n=(n-1)^2+(2n-1)$.

Note: This answer is not intended to be particularly useful or even mathematically revealing. It is certainly not the most beautiful way of establishing the identity (the use of induction disqualifies it immediately), but I thought it was a nice way of showing the inductive step, without having to multiply out the brackets.

Answer 10

you can see this link in generally solution :

http://en.wikipedia.org/wiki/Arithmetic_progression

This section is about Finite arithmetic series. For Infinite arithmetic series, see Infinite arithmetic series.

The sum of the members of a finite arithmetic progression is called an arithmetic series.

Expressing the arithmetic series in two different ways:

$ S_n=a_1+(a_1+d)+(a_1+2d)+\cdots+(a_1+(n-2)d)+(a_1+(n-1)d)\\ S_n=(a_n-(n-1)d)+(a_n-(n-2)d)+\cdots+(a_n-2d)+(a_n-d)+a_n.$

Adding both sides of the two equations, all terms involving d cancel:

$ \ 2S_n=n(a_1+a_n).$

Dividing both sides by 2 produces a common form of the equation:

$ S_n=\frac{n}{2}( a_1 + a_n).$

An alternate form results from re-inserting the substitution:$ a_n = a_1 + (n-1)d:$

$ S_n=\frac{n}{2}(2a_1 + (n-1)d). $