An intuitive definition of the frequency spectrum of a function.

Question

In a PDE book I'm reading, the author introduces the Fourier transform by first introducing the Fourier series, and then the Fourier integral representation of a function. The Fourier integral representation is given by

$$f(x)=\int_0^{\infty}a(\xi)\cos(\xi x)\mathbb d\xi +\int_0^{\infty} b(\xi)\sin(\xi x)\mathbb d\xi$$

where

$$a(\xi)=\frac 1{\pi}\int_0^{\infty}f(x)\cos(\xi x)\mathbb dx$$

$$b(\xi)=\frac 1{\pi}\int_0^{\infty}f(x)\sin(\xi x)\mathbb dx$$

Now, the frequency spectrum $C(\xi)$ of a function $f(x)$ is defined as

$$C(\xi)=\sqrt{a^2(\xi)+b^2(\xi)}$$

The author proceeds to give some examples, shown below:

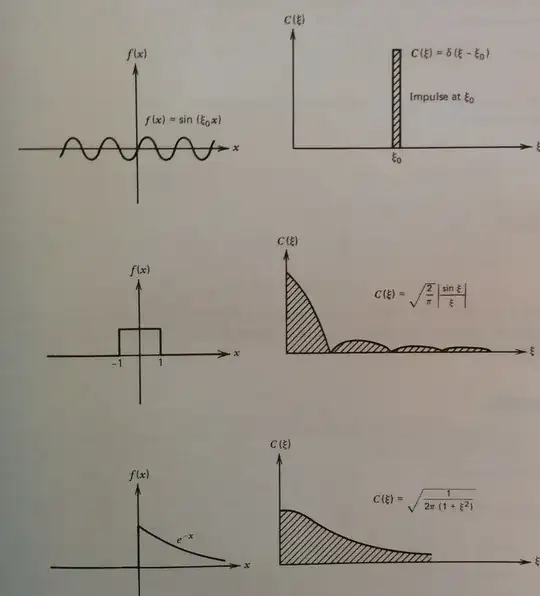
Now, while I understand this mathematically, my intuition is severely lacking. My question is:

What is an intuitive way to think about the frequency spectrum of a function?

Answer 1

IMHO Intuition is generally more an aesthetic cherry on the top kind of thing, but here you go.

Generally speaking, all integral transforms do is weight a function according to some kernel, namely another function.

In the Fourier transform, a time domain is weighted according to a frequency domain. In other words, sine waves, become scalars that show how much of a frequency is present in a particular function.

Look here for more intuition and information.

To explicitly answer your question, for the frequency spectrum. You find the Euclidean distance function of two integral transforms, which is just the Fourier transform.

Answer 2

The frequency spectrum gives you the amplitudes for every frequency from DC to daylight that are required in order to reconstruct the original function. The only complication is that the frequency phase shift has to be accounted for as well. That's why you need sin and cosine function: $$ \sin(\omega t + \phi) = \cos(\phi)\sin(\omega t)+\sin(\phi)\cos(\omega t). $$ The phase shift can be achieved by adding the correct combination of $\sin$ and $\cos$ terms of the same frequency. To see why this interpretation is reasonable, suppose that the Fourier transform is smooth. Then $f$ can be approximated by a Riemann sum (the inverse transform,) which is a finite linear combination of the various frequencies, where the total weights remain finite as you take a finer and finer Riemann approximation. For example, if $a$ and $b$ are integrable, then $$ f(x)=\int_{0}^{\infty}\{a(\xi)\cos(\xi x)+b(\xi)\sin(\xi x)\}d\xi \\ \approx \int_{0}^{R}\cdots d\xi \approx \sum_{n=1}^{N-1}a(\frac{Rn}{N}\xi)\cos(\frac{Rn}{N}\xi)+b(\frac{Rn}{N}\xi)\sin(\frac{Rn}{N}\xi). $$ You can write $a(\frac{Rn}{N}\xi)\frac{R}{N}=a_{n}$, $b(\frac{Rn}{N}\xi)\frac{R}{N}=b_{n}$ and $$ f(x) \approx \sum_{n=0}^{N-1}a_n\cos(\frac{Rn}{N}\xi)+b_{n}\sin(\frac{Rn}{N}\xi) $$ If $a_n^{2}+b_{n}^{2}\ne 0$, then there exists $\phi_n$ such that $$ \frac{a_n}{\sqrt{a_n^{2}+b_n^{2}}}=\sin(\phi_n),\;\;\frac{b_n}{\sqrt{a_n^{2}+b_n^{2}}}=\cos(\phi_n) $$ because $$ \left(\frac{a_n}{\sqrt{a_n^{2}+b_n^{2}}}\right)^{2} +\left(\frac{b_n}{\sqrt{a_n^{2}+b_n^{2}}}\right)^{2}=1. $$ That gives $$ f(x) \approx \sum_{n=0}^{N-1}\sqrt{a_n^{2}+b_n^{2}}\sin(\frac{Rn}{N}x+\phi_n). $$ So $\sqrt{a(\xi)^{2}+b(\xi)^{2}}d\xi$ is the amplitude of the frequencies in the range $(\xi,\xi+d\xi)$. At least in principle, you can write $$ f(x)=\int_{0}^{\infty}\sqrt{a(\xi)^{2}+b(\xi)^{2}}\sin(\xi x+\phi_{\xi})d\xi, $$ which can be thought of as a continuous sum of pure frequency modes with phase shifts $\phi_{\xi}$ and amplitudes $\sqrt{a(\xi)^{2}+b(\xi)^{2}}$.