10

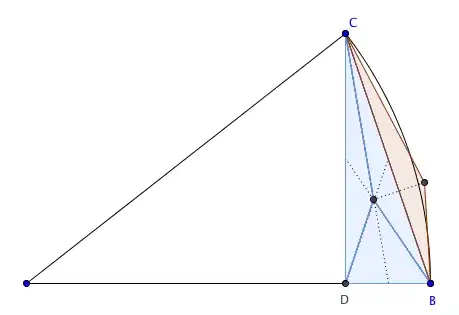
While looking at this question, I noticed an interesting geometric interpretation of the limit the OP was trying to evaluate. His limit came to twice the value of the limit

$$\lim_{x\to 0}\frac{\sin x (1-\cos(x))}{x-\sin x}$$

which can be interpreted as the limit of the ratio of the area of $\triangle DBC$ and the area bounded between the line $CB$ and the arc $CB$. (See the image below).

enter image description here

I know that the limit $\lim_{x\to 0} \frac{\sin x}{x} = 1$ is often derived through a geometric method. Can this the limit I've given be evaluated geometrically?

Community
  • 1
  • 1
    This is an exercise in Stewart. It can of course be done by L'Hopital's rule, but L'H's rule, although it may find the answer very efficiently, often doesn't give much if any insight. – Michael Hardy Jul 07 '15 at 05:38
  • If we let $f(x) = x - \sin x$, then the original limit is $\lim_{x \to 0} [f(2x)/f(x) - 2]$. So in order to calculate the limit, it is enough to establish that $f(x) \sim ax^3$ for some nonzero $a$. We don't need to know that $a = 1/6$. I'm not sure whether this makes things any easier. – Keith Jul 07 '15 at 06:06

2 Answers2

3

Not sure how convincing this is, but consider: enter image description here

That point in the middle of trangle $DBC$ is its centroid, so that all three subtriangles have the same area. Does the area of the upper right subtriangle approximate the area of the arc sliver to a high enough degree as the angle approaches $0$? If so, the ratio is of course $3$.

2'5 9'2
  • 54,717
  • Visually it looks convincing but this is not as rigorous as the proof of $(\sin x)/x \to 1$ as $ x \to 0$ given at http://math.stackexchange.com/a/75151/72031 I believe it is impossible to find a geometric rigorous proof of this limit as it is equivalent to the limit $(x - \sin x)/x^{3} \to 1/6$ as $x \to 0$ and this is one is notoriously difficult to prove without using derivatives. – Paramanand Singh Jul 07 '15 at 11:45
  • 1
    On the other hand thanks for such nice figure which at gives some informal argument that the value of limit should be 3. +1 – Paramanand Singh Jul 07 '15 at 11:46
-1

I think this limit is impossible to evaluate geometrically, at least using the squeeze theorem. First, note that the area of $∆ACB=sinx/2$ because the area of a triangle is $bh/2$ with $b=1$ and $sinx=h$ in this case. Also, $∆ADC=sin(x)cos(x)/2$ and the area of the sector is $x/2$. Thus, to use the Squeeze Theorem, we would need this inequality:

$sinxcosx/2 < sinx/2 < x/2$

The problem is that this inequality only holds true in quadrant 1 where everything is positive, but in order to take the limit as x goes to 0, we need to evaluate the limit from quadrant 4 because we take the limit from left to right. But because sinx is negative in quad 4, the inequality no longer holds true. Obviously, we would need to majorly rewrite the inequality before we can even take the limit, but I strongly suspect that we'd still have the same problem. In fact, I suspect that no matter how we set up the inequality, this problem still remains. So I doubt you can evaluate this limit geometrically, using basic methods anyway.

kopse
  • 57