Evaluate $\lim\limits_{x\to 0} \frac{x(1-\cos x)}{x - \sin(x)}$ without Taylor series or L'Hôpital's rule?

Question

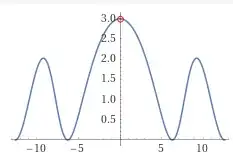
I want to evaluate $\lim\limits_{x\to 0} \frac{x(1-\cos x)}{x - \sin(x)}$. We know that its plot is:

And also with attention to the Taylor series we know that its series expansion at $x=0$ is:

$$3 - x^2/10 - x^4/4200 + O(x^6)$$

So the limit is $3$. But I want to evaluate it without Taylor series or L'Hôpital's rule.

What I tried: $$\begin{aligned} \lim\limits_{x\to 0} \frac{x(1-\cos x)}{x - \sin(x)}& =\\ &\lim_{x\to 0}\frac{x\cdot2\sin^2\frac{x}{2}}{x - \sin x} = \lim_{x\to 0}\frac{2x\cdot\sin^2\frac{x}{2}}{x\cdot(1 - \frac{\sin x}{x})} = \\&\lim_{x\to 0}\frac{2\sin^2\frac{x}{2}}{1 - \frac{\sin x}{x}} \end{aligned}$$ But that did not help to evaluate the indeterminate form. Also I want to know is there a geometric representation for $x - \sin(x)$ which helps us to evaluate the limit?

Answer 1

Use two standard limits:

(1) $\lim_{x\to0}\frac{1-\cos x}{x^2}=\frac{1}{2}$

(2) $\lim_{x\to0}\frac{x-\sin x}{x^3}=\frac{1}{6}$

So your question is nothing but ratio of two:

Proof of (1) $$\lim_{x\to0}\frac{1-\cos x}{x^2}=\lim_{x\to0}\frac{2\sin^2(\frac{x}{2})}{x^2}=\frac{1}{2}\lim_{x\to0}(\frac{\sin(\frac{x}{2})}{\frac{x}{2}})^2=\frac{1}{2}$$

Proof of (2)

$$L=\lim_{x\to0}\frac{x-\sin x}{x^3}$$ $$\Rightarrow L=\lim_{x\to0}\frac{3x-\sin(3x)}{(3x)^3}$$

$$\Rightarrow L=\lim_{x\to0}\frac{3x-3\sin x+4 \sin^3 x}{27x^3}$$ $$\Rightarrow L=\frac{L}{9}+\frac{4}{27}\lim_{x\to0}(\frac{\sin x}{x})^3$$ $$\Rightarrow \frac{8L}{9}=\frac{4}{27}$$ $$\Rightarrow L=\frac{1}{6}$$

Answer 2

Too long for a comment: An Idea for the geometric meaning question of OP.

In freshman level calculus we proved the limits $\lim_{x\to 0}\frac{\sin x}x=1\tag 0$ and $\lim_{x\to 0}\frac{1-\cos x}{x^2}=\frac12\tag1$ geometrically by using the sector $\widehat{OPA}$ of the unit circle where $O$ is the origin, $P=(\cos x,\sin x)$ and $A=(1,0)$. The area of this sector minus the area of the triangle $\triangle OPA$ is equal to $\frac{x-\sin x}2$. We can approximate this difference area by drawing equally spaced $n$ chords (or tangent lines) on the arc and constructing a polygon. The resulting expression will be a function of $\cos(\frac x{2n})$ and $\sin(\frac x{2n})$ in chord way. Dividing by $x^3$ and taking the limit $x\to 0$ and $n\to\infty$ we can find the limit $\frac{1}{12}$ by using $(0)$ and $(1)$ only. Indeed, I did this with three tangent lines and obtained $\frac{3}{32}$ which is an upper bound for $\frac{1}{12}$. Hence, $\lim_{x\to 0}\frac{x-\sin x}{x^3}=\frac16\tag2$ The answer of the question:

$\lim\limits_{x\to 0} \frac{x(1-\cos x)}{x - \sin x}=$$\lim\limits_{x\to 0} \frac{\frac{1-\cos x}{x^2}}{\frac{x - \sin x}{x^3}}=\frac{\frac12}{\frac16}=3.$

Answer 3

Addition to the answer of @deep dm. We know that $\sin' = \cos$ and $\cos' = -\sin$.

Let $f(x) = \sin x-x$. Since $f(0) = 0$ and $f'(x) = \cos(x)-1\le 0$ for $x\in[0, \frac{\pi}{2}]$, by MVT $f(x)\le 0$ for $x\in[0, \frac{\pi}{2}]$.

Similarly, let $g(x) = \cos(x)-1+\frac{x^2}{2}$. $g(0) = 0$ and $g'(x) = -\sin x+x = -f(x)\ge 0$ for $x\in[0,\frac{\pi}{2}]$, by MVT we have $g(x)\ge 0$ for $x\in[0, \frac{\pi}{2}]$.

Again, let $h(x) = \sin(x)-x+\frac{x^3}{6}$. $h(0) = 0$ and $h'(x) = g(x)\ge 0$ for $x\in[0, \frac{\pi}{2}]$ and $h(x)\ge 0$ for $x\in[0, \frac{\pi}{2}]$.

Doing this stuff two times more, one obtains $x-\frac{x^3}{6}\le\sin x\le x-\frac{x^3}{6}+\frac{x^5}{24}$. This is enough to conclude that the limit (2) is $\frac{1}{6}$.

It may seem dificult to find right coefficient(actually, they are Taylor coefficients). One may use integration(define $g(x) = -\int_0^x f(t)dt$, etc.) instead of MVT, then the coefficients arise naturally, too.