Intersection of translated simple curves in $\mathbb{R}^2$

Asked Jun 12 '15 at 15:52

Active Jun 12 '15 at 22:12

Viewed 126 times

I'm trying to prove the following conjecture:

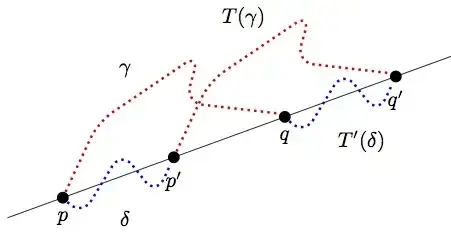
Let $\gamma$ be a simple (i.e. non self-intersecting) plane curve going from point $p$ to $q$. Let $T(\gamma)$ be a translated copy of $\gamma$ going from point $p'$ to $q'$.

Now, consider another simple plane curve $\delta$ from point $p$ to $p'$. Let $T'(\delta)$ be a translated copy of $\delta$ going from point $q$ to $q'$.

If the points $p$, $p'$, $q$ and $q'$ are collinear in this order, then the curve $\Gamma=\gamma \cdot T'(\delta)\cdot T(\gamma)^R\cdot \delta^R$ self-intersects.

Here, $R$ is the reversal operator and «$\cdot $» is the concatenation operator.

enter image description here

I already looked into intersection theory and self-intersection number of curves but I'm not well versed in algebraic geometry. I also tried different approaches based on topological ideas (e.g. finding homeomorphisms with circles) but to no avail.

Any help, tips or counter-examples would be appreciated. Thanks!

edited Jun 12 '15 at 22:12

asked Jun 12 '15 at 15:52

Hugo Tremblay

1

$\gamma(p)=p$ does not make sense, since $\gamma(p)$ needs to be a member of $\mathbb R^2$ and $p$ isn't if the notation $[p,q]$ is to be valid. – hmakholm left over Monica Jun 12 '15 at 15:54
Your notations simply do not make sense. – Alex M. Jun 12 '15 at 16:33
Indeed it doesn't make sense. I edited the question. I hope it is clearer now. – Hugo Tremblay Jun 12 '15 at 17:48

Intersection of translated simple curves in $\mathbb{R}^2$

0 Answers0

Linked