5

I just learned a tiny bit about SIA. While it is interesting, that it handles derivatives so easily, I wonder:

Can we still recover the concepts of limits (of sequences) and especially series, to make statements like:

  • $\lim_{n\to \infty} (1+\frac{1}{n})^n = e$
  • $\sum_{k=1}^\infty \frac{1}{k} = \infty$
  • $e^x = \sum_{k=0}^\infty \frac{x^k}{k!}$

and so on and so forth? I didn't find anything about this.

Stefan Perko
  • 12,467
  • @user3491648 "btw you don't have limits in the smooth reals." Yes, I figured as much. But since said answer made some interesting points, pointed me to some other sources and was literally the only answer, I figured "what the heck". --- On another note: Maybe I should have been clearer about this: I didn't think we could have literal limits in SIA (in the classical sense), just some statements, that intuitively mean the same thing. – Stefan Perko Jun 13 '15 at 21:10
  • The first one. –  Jul 22 '16 at 23:48

1 Answers1

3

Relation to Smooth Infinitesimal Analysis

Stanford Encyclopedia of Philosophy discusses Smooth Infinitesimal Analysis (using nilpotent $\epsilon^n = 0$, not just $\epsilon^2 = 0$ as in the above discussion) in contrast to non-standard analysis (using hyperreals). In fact, SIA is very close to how Theoretical Physicists manipulate infinitesimal quantities, to the accuracy they desire.

Depending on how much details you want, the construction of these infinitesimals involves sheaves and toposes, and the principle of microaffineness.

Stanford Enclycopedia includes this startling comment:

We observe that the postulates of smooth infinitesimal analysis are incompatible with the law of excluded middle of classical logic.

This [blog] uses infinitesimals but they only go to second order $dx^2 = 0$. Introductory books on Calculus have been written using both approaches:

For more advanced reading, some students have wrtten Master's Theses ont he topic:

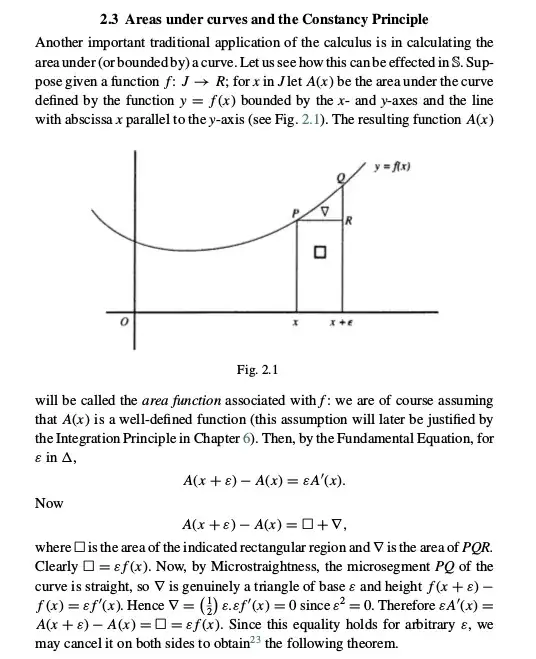
Taylor's Theorem

Using SIA a form of Taylor's theorem is exact since we choose $\epsilon^n = 0$

$$ f(x+\epsilon) = \sum_{k=0}^n f^{(k)}(x) \frac{\epsilon^k}{k!} $$

Therefore we can show the derivative of the exponential function is itself in SIA and expand:

$$ (e^x)'= e^x \hspace{0.125in}\text{ and }\hspace{0.125in} e^\epsilon = \sum_{k=0}^n \frac{\epsilon^k}{k!} \hspace{0.125in}\text{ or }\hspace{0.125in} e = \lim_{n \to \infty} (1 + \epsilon)^n $$

In general, this seems to be a way of obtaining infinite series as the Taylor series expansion and there is duality between $\epsilon \leftrightarrow n$.

COMMENT Upon further investigation, there doesn't seem to be any analogue of the Mean Value Theorem or Intermediate Value Theorem (which is provable in nonstandard-analysis). So in theory we can't prove:

Intermediate Value Let $a < b$ and $f(a) > 0$ and $f(b) < 0$, then there exists $a < c < b$ such that $f(c) = 0$ (False in $\mathbb{S}$)

This result breaks down in SIA - related to the Law of Excluded Middle. The Mean Value Theorem and (global) Taylor's Theorem seems to enjoy similar fates.

While we can take deritives (and integrals!) there doesn't seem to be any way to connect local and global information in the smooth world $\mathbb{S}$.

Divergence of Harmonic Series $\sum \frac{1}{k} = \infty$

The standard way to prove the divergence of Harmonic series is to use the integral test which states that if $f$ is monotone decreasing then

$$ \int_0^\infty f(x) \, dx < \sum_{k=0}^\infty f(k) < f(0) + \int_0^\infty f(x) \, dx$$

In our cases $f(x) = \frac{1}{x}$ but how to we know the integral test works in SIA? What is an integral? Bell's Primer of Infinitesimal Calculus defines $\mathbf{\color{blue}{\int}}$ rather obliquely as the "area under the curve" but now you're done.

enter image description here

cactus314
  • 24,438
  • As I understand, in the SIA framework, Taylor's theorem to each finite order $N$ works by taking $\epsilon$ with $\epsilon^k \neq 0$ for $k \leq N$ but $\epsilon^{N+1}=0$. Then $f(x+\epsilon)-f(x)$ involves the first $N$ derivatives (and no error term). – Ian Jun 08 '15 at 19:37
  • @Ian I am not fimiliar with this version of non-standard analysis, so I am outlining some of the things that are going wrong when I try to help him. – cactus314 Jun 08 '15 at 19:38
  • What you've written is reasonable. I'm pointing out the main effect that you're missing, which is that not all SIA infinitesimals are nilsquare. The nilsquare infinitesimals are used for isolating linear-order effects (in the classical sense). Meanwhile the nilcube infinitesimals are used for isolating quadratic-order effects (in the classical sense). And so on. – Ian Jun 08 '15 at 19:40
  • @StefanPerko judging from your question you know nothing about infinitesimal analysis. so why don't you make your question more specific? – cactus314 Jun 08 '15 at 20:06
  • @johnmangual I gave you the bounty, since this seems to be a good answer, considering what one can find out trough books and notes. Also, it's nice since I was not familiar with all the sources. But: Could you please clarify / correct the "Taylor's theorem" part? I think you are missing a $1/k!$. I also think your formula of $e^\epsilon$ is missing an $\epsilon^k$. Finally, I don't know, what $e = \lim_{n\to \infty} (1+\epsilon)^n$ means... – Stefan Perko Jun 13 '15 at 15:59
  • @StefanPerko I looked into it further. With these type of "nilpotent" infinitesimals, $\epsilon$ is not really "small" it just vanishes to a certain order. More specifically, the Intermediate Value Theorem is false. Likewise, many of the series and limit definitions you have defined may not work in SIA. – cactus314 Jun 14 '15 at 17:28