What is the maximum volume of $N$-D slice of an $M$-D hypercube?

Question

Consider a unit hypercube of M dimensions. We wish to make a cut of dimension N through it. What is the largest N-D size (length, area, volume, ...) we can achieve, $S(M, N)$, and what cut gives it?

Examples:

• $S(M=2, N=1) = \sqrt2$
  • Linear cut through a square
  • Largest slice is the diagonal
  • Length $\sqrt{1^2 + 1^2}$
• $S(M=3, N=1) = \sqrt3$
  • Linear cut through a cube
  • Largest slice is the space diagonal
  • Length $\sqrt{1^2 + 1^2 + 1^2}$
• $S(M=3, N=2) = \sqrt 2$
  • Planar cut through a cube
  • Largest slice is the plane through the diagonal
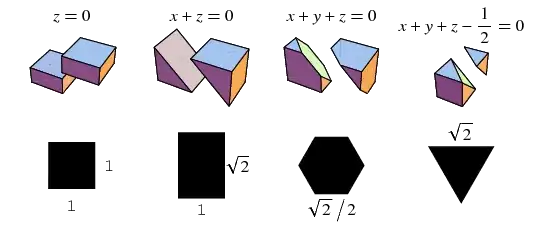
  • Area $\sqrt 2 \cdot 1$

Bits of this function are easy to generalize: $$ S(M, N) = \left\{ \begin{array}{rl} \sqrt M & : N = 1\\ ? & : 1 < N < M\\ 1 & : N = M\\ 0 & : N > M\\ \end{array} \right. $$

Can we generalize for $N = 2, 3, ...$?

Answer 1

$S(M,M-1)=\sqrt{2}$ for all $M\ge1$; this is a theorem of Keith Ball from 1986.

$S(4,2)$ is the smallest term not specified by this result; it is at least $2$, by taking the plane $x_1=x_2, x_3=x_4$, which forms a $\sqrt{2}\times\sqrt{2}$ square. I suspect this is optimal, but I don't see an easy way to prove it.

Answer 2

Just to put into words, without proof, the idea that has been floating around here.
Let $M=aN+b$.
Split the $M$ dimensions into $b$ groups of $a+1$ and $N-b$ groups of $a$.
Take the diagonal in each group, of length $\sqrt a$ or $\sqrt{a+1}$.
The product of all these diagonals is $$\sqrt{a^{N-b}(a+1)^b}$$

Answer 3

As a lower bound $S(M, N) \ge \sqrt{M - N + 1}$

where the slice is a $\underbrace{1 \times 1 \times \cdots}_{N-1} \times \sqrt{M - N + 1}$ cuboid

---

Choose the first $N-1$ axes of the hypercube to lie in the slice-space. (Possibly non-optimal)

A $M - N + 1$ subspace remains, from which we want to find the longest 1-area.

This is $S(M - N + 1, 1) = \sqrt{M - N + 1}$.