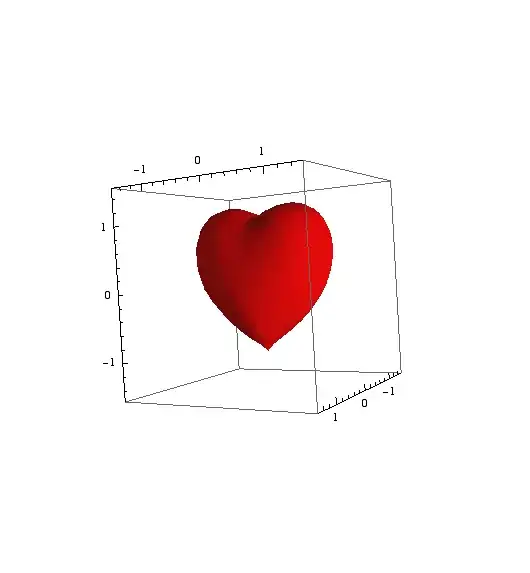
A three-dimensional space curve with the shape of a red heart:

The Mathematica code for the image above is:
ParametricPlot3D[{Cos[u]*(4*Sqrt[1 - v^2]*Sin[Abs[u]]^Abs[u]), v,
Sin[u]*(4*Sqrt[1 - v^2]*Sin[Abs[u]]^Abs[u])},
{u, -Pi, Pi}, {v, -1, 1}, Axes -> None, Mesh -> False,
Boxed -> False,
PlotStyle -> {Red, Specularity[White, 10]}]
3D red heart with Mesh and lines:

Mathematica code for the image above:
ParametricPlot3D[{Cos[u]*(4*Sqrt[1 - v^2]*Sin[Abs[u]]^Abs[u]), v,
Sin[u]*(4*Sqrt[1 - v^2]*Sin[Abs[u]]^Abs[u])}, {u, -Pi,
Pi}, {v, -0.97, 0.97}, PlotPoints -> 50, Axes -> None,
Boxed -> False,
PlotStyle ->
Directive[Glow[Red], Specularity[White, 30], Opacity[0.15]],
Mesh -> 50, Background -> Black, MeshStyle -> {Blue, Red},
Lighting -> {{"Directional", Yellow, {{1.5, 1.5, 5}, {1.5, 1.5, 0}},
Pi/6}}]
A variation on the use of the Taubin heart surface with hue:

Mathematica code for the last image above:
ContourPlot3D[(-1/10) x^2 z^3 -
y^2 z^3 + (2 x^2 + y^2 + z^2 - 1)^3 == 0, {x, -1.2, 1.2}, {y, -1.4,
1.4}, {z, -1.5, 1.5}, Mesh -> False, PlotPoints -> 60,
Axes -> None, Boxed -> False,
ContourStyle -> Directive[Opacity[0.5], Red],
ColorFunction -> Function[{x, y, z, f}, Hue[z]]]
For more customized heart images, see the post in my website/blog:
https://knowledgemix.wordpress.com/2014/02/14/heart-to-heart-with-3d-math/
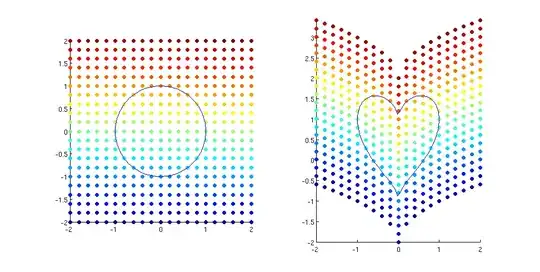
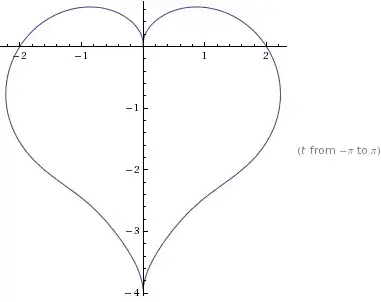
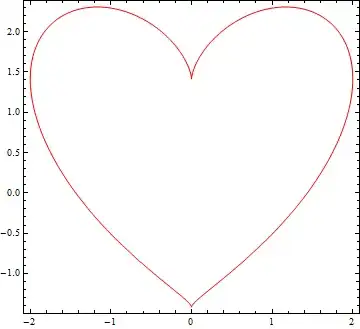
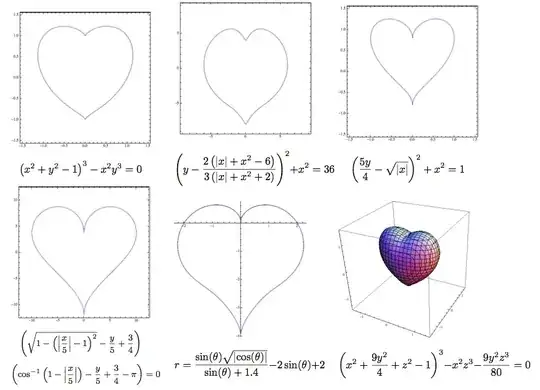





http://xahlee.org/SpecialPlaneCurves_dir/Cardioid_dir/cardioid.html
http://demonstrations.wolfram.com/GeneratingACardioidIIICirclesPassingThroughAPoint/
There is also a differential geometry with mathematica book you may want to look up if the links don't give you what you are looking for.
– WWright Nov 27 '10 at 19:41SphericalPlot3D[Log[u] + Sin[v], {u, 0, 2 Pi}, {v, 0, 2 Pi}]– Yaroslav Bulatov Nov 28 '10 at 02:22