Which function is appropriate for the geometrical shape mostly used as LOVE symbol

Question

I tried $\;r=-1-\sin\theta,\,$ for $\,\theta$ between $[-2\pi,2\pi]$. But it's not as accurate as expected.

Any one to help me?

Thank you in advance.

Somehow related: http://math.stackexchange.com/questions/54506/is-this-batman-equation-for-real — Hagen von Eitzen, Jul 07 '13 at 15:53

amWhy · Answer 1 · 2013-07-07T14:35:34.807

13

You can use the union of $$y = |x| + \sqrt{1 - x^2} \quad \cup \quad y = |x| - \sqrt{1 - x^2}$$ to obtain the following (compliments of Wolfram):

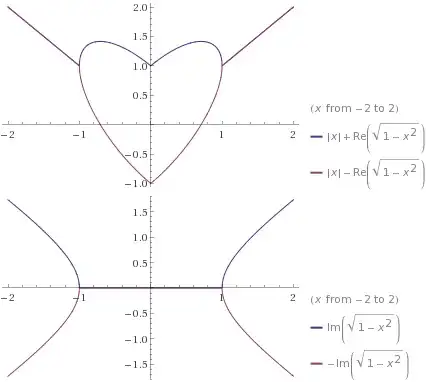
enter image description here

Then perhaps tweak the "domain" to obtain the desired figure.

Search Wolfram Alpha by typing heart curve in the input field: you'll find some heart curves to select from in a drop down menu.

For example, using $$(x^2 + y^2 - 1)^3 = x^2y^3$$ You'll obtain the following graph:

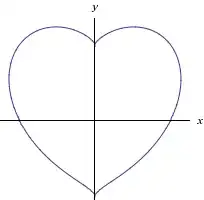
enter image description here

I couldn't resist also adding this:

If you want the "real thing": an anatomical heart: See this link for a very complex function that will yield the following graph!:

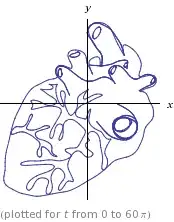
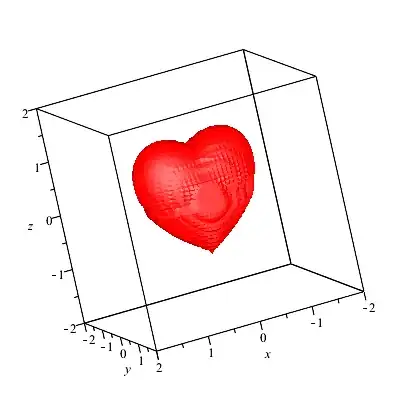
enter image description here

edited Jul 07 '13 at 14:35

answered Jul 07 '13 at 14:21

amWhy

209,954

The $(x^2+y^2−1)^3 = x^2y^3$ that you mentioned from WolframAlpha looks nice as a curve, but it has some discontinuities (?) at $y=0$ that make it less useful for anything involving derivatives. – LarsH Feb 15 '18 at 14:14

score 3 · Answer 2 · answered Jul 07 '13 at 14:15

3

How about $y=|x|\pm \sqrt{1-x^2}$

answered Jul 07 '13 at 14:15

Empy2

50,853

Mikasa · Accepted Answer · 2013-07-08T17:05:47.273

3

I love this one which is from one of my old works in Maple. There is another function in it:

> with(plots);
> plot([16*sin(t)^3, 13*cos(t)-5*cos(2*t)-2*cos(3*t)-cos(4*t), t = 0 .. 6.3], thickness = 3);
> implicitplot3d((x^2+9*y^2*(1/4)+z^2-1)^3-x^2*z^3-9*y^2*z^3*(1/80) = 0, x = -2 .. 2, y = -2 .. 2, z = -2 .. 2, axes = boxed, numpoints = 100000, color = red);

enter image description here