Does there exists a closed form of$$ \displaystyle \int _{ 0 }^{ \pi /2 }{ x\sqrt { \tan { x } } \log { (\cos { x } ) }\ dx }$$
If exists can someone find a way to tackle this integral and provide a closed-form of it. Many similar integrals have closed form and I believe this one, too.
Substitute $t = \sqrt{\tan x}$
\begin{align} I=\int_{0}^{\pi/2}x\sqrt{\tan{x}}\ln({\cos x})\ dx=J(1)\\ \end{align} where $J(a)= -\int_0^\infty \frac{t^2 \ln(1+t^4) \tan^{-1}(a^2t^2)}{1+t^4}dt$ \begin{align} J’(a)=&-\int_0^\infty \frac{2at^2 \ln(1+t^4)}{(1+t^4)(1+a^4t^4)}dt\\ =& \ \frac{2a}{1-a^4}\int_0^\infty \left(\frac{\ln(1+t^4)}{1+t^4}- \frac{\ln(1+t^4)}{1+a^4t^4} \right)dt \end{align} Let $K(a,b)=\int_0^\infty \frac{\ln(1+b^4t^4)}{1+a^4t^4}dt$
\begin{align} K_b’(a,b)=&\int_0^\infty \frac{4b^3 t^4}{(1+a^4t^4)(1+b^4t^4)}dt =\frac{\sqrt2\pi b^2}{a(a+b)(a^2+b^2)} \end{align}
Then \begin{align} K(a,b)= &\int_0^b K_b’(a,s)ds = \frac\pi{\sqrt2 a}\left(\frac12\ln\frac{a^2+b^2}{a^2} +\ln\frac{a+b}a-\tan^{-1}\frac ba\right)\\ J’(a)=&\ \frac{2a}{1-a^4}\left[K(1,1)-K(a,1) \right]\\ =& \frac{\sqrt2\pi}{1-a^4} \left[a\left(\frac32\ln2-\frac\pi4 \right)-\frac12 \ln\frac{1+a^2}{a^2} -\ln\frac{1+a}{a}+\cot^{-1}a \right] \end{align} and
\begin{align} I=&\ J(1)=\int_0^1 J’(a)da\\ =& -\sqrt2\pi \bigg[ \left(\frac32\ln2-\frac\pi4 \right)\int_0^1 \frac{1-a}{1-a^4}da +\frac12\int_0^1 \frac{\ln\frac{1+a^2}{2a^2}}{1-a^4}da\\ &\>\>\>\>\>\>\>\>\>\>\>\>\>\>\> +\int_0^1 \frac{\ln\frac{1+a}{2a}}{1-a^4}da +\int_0^1 \frac{\frac\pi4-\cot^{-1}a}{1-a^4}da\bigg]\\ =& -\sqrt2\pi \bigg[ \left(\frac32\ln2-\frac\pi4 \right)\left(\frac\pi8+\frac14\ln2\right) +\frac12\left(\frac12G+\frac{3\pi^2}{32} +\frac\pi{8}\ln2 \right)\\ &\>\>\>\>\>\>\>\>\>\>\>\>\>\>\> +\left(\frac12G+\frac{\pi^2}{24} -\frac\pi{16}\ln2\right) +\left(-\frac14G-\frac{\pi^2}{64}\right)\bigg]\\ =&-\frac\pi{\sqrt2}\left(G+\frac{\pi^2}{12}+\frac\pi4\ln2+\frac34\ln^22 \right) \end{align}
By enforcing the substitution $x\mapsto\arctan(x)$, we can rewrite to the integral
$$\mathcal I = \int_0^{\frac\pi2} x \sqrt{\tan(x)} \log(\cos(x)) \, dx = -\frac12 \int_0^\infty \frac{\sqrt x \arctan(x) \log(1+x^2)}{x^2+1} \, dx$$
which we can try to evaluate using the same approach for determining $\int\limits_0^\infty\frac{\log(x)\arctan(x)}{x^2+1}\,dx=\frac78\zeta(3)$.
Let $$I(b) = \int_0^\infty \frac{\sqrt x \arctan(x) \log(x^2+1)}{x^2+b^2} \, dx$$
and $f(z)=\dfrac{\sqrt z \arctan(z) \log(z^2+1)}{z^2+b^2}$ with real parameter $0<b<1$. Note that
$$\begin{align*} \sqrt z &= |z|^{\frac12} e^{i \frac12\arg(z)} \\[1ex] \arctan(z) &= -\frac i2 \log\left(\frac{i-z}{i+z}\right) \\ &= -\frac i2 \log\left|\frac{i-z}{i+z}\right| + \frac12 \arg\left(\frac{i-z}{i+z}\right) \\[1ex] \log(1+z^2) &= \log(z-i) + \log(z+i) \\ &= \log|z^2+1| + i \left(\arg(z-i) + \arg(z+i)\right) \end{align*}$$
Take branch cuts at $[0,\infty)$ (due to $\sqrt z$) as well as $\pm[i,i\infty)$ (due to the other logarithms), so that
$$\begin{cases}\arg(z)\in(0,2\pi) \\ \arg\left(\frac{i-z}{i+z}\right) \in (-\pi,\pi) \\ \arg(z-i)+\arg(z+i) \in (-\pi,\pi)\end{cases}$$
Now consider the contour integral $\oint_{\mathcal C} f(z) \, dz$ over the same positively oriented circular path $\mathcal C$ specially deformed to avoid the branch points. Let
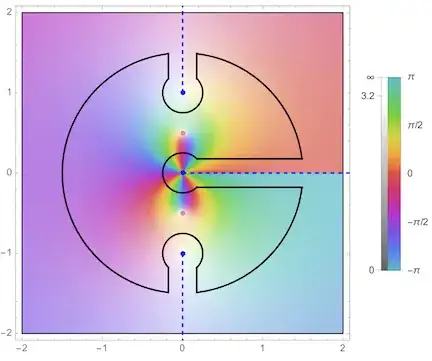
It's fairly easy to show the integrals over $\Gamma$ and $\gamma_{1,2,3}$ vanish as $R\to\infty$ and $\varepsilon\to0$.
Parameterize the remaining component contours as follows.
$$\begin{array}{c|ccc} A & z = x + i\varepsilon & x\in[\varepsilon,R] & dz = dx \\ A' & z = x - i\varepsilon & x\in[R,\varepsilon] & dz = dx \\ \hline B & z = \varepsilon + iy & y\in[1+\varepsilon,R] & dz = i\,dy \\ B' & z = -\varepsilon + iy & y\in[R,1+\varepsilon] & dz= i\,dy \\ \hline C & z = -\varepsilon - iy & y\in[1+\varepsilon,R] & dz = -i\,dy \\ C' & z = \varepsilon - iy & y\in[R,1+\varepsilon] & dz = -i\,dy \end{array}$$
On the banks of each cut, as $\varepsilon\to0$ we pick up
The integrals around each cut, and hence the overall contour integral, converge to
$$\begin{align*} \int_{A\cup A'} f(z) \, dz &\to 2 \int_0^\infty \frac{\sqrt x\,\arctan(x)\log(x^2+1)}{x^2+b^2} \, dx \\[2ex] \int_{B\cup B'} f(z) \, dz &\to i \pi e^{i\frac\pi4} \int_1^\infty \frac{\sqrt y}{y^2-b^2} \left(\log\left(y^2-1\right) + \log\left(\frac{y-1}{y+1}\right)\right) \, dy \\[2ex] \int_{C\cup C'} f(z) \, dz &\to i \pi e^{i\frac{3\pi}4} \int_1^\infty \frac{\sqrt y}{y^2-b^2} \left(\log\left(y^2-1\right) - \log\left(\frac{y+1}{y-1}\right)\right) \, dy \end{align*}$$
and simplifying integrands with
$$\begin{align*} \log(y^2-1) + \log\left(\frac{y-1}{y+1}\right) &= \bigg(\log(y-1)+\log(y+1)\bigg) + \bigg(\log(y-1) - \log(y+1)\bigg) \\[1ex] &= 2 \log(y-1) \end{align*}$$
$$\begin{align*} \implies \oint_{\mathcal C} f(z) \, dz &\to 2\,I(b) - \pi\sqrt2 \int_1^\infty \frac{\sqrt y}{y^2-b^2} \log(y-1) \, dy \\[1ex] &= 2\,I(b) - \frac{\pi\sqrt2}{\sqrt b} \int_0^b \frac{\log(b-y)-\log(y)}{\sqrt y(1-y^2)} \, dy \end{align*}$$
where we substitute $y \mapsto \frac by$.
At the poles, we have residues
$$\begin{align*} \underset{z=ib}{\operatorname{Res}} f(z) &= \lim_{z\to ib} (z-ib) f(z) = -\frac{e^{i\frac\pi4} \log\left(\frac{1-b}{1+b}\right) \log\left(1-b^2\right)}{4\sqrt b} \\[1ex] \underset{z=-ib}{\operatorname{Res}} f(z) &= \lim_{z\to -ib} (z+ib) f(z) = \frac{e^{i\frac{3\pi}4} \log\left(\frac{1+b}{1-b}\right) \log\left(1-b^2\right)}{4\sqrt b} \end{align*} \\ \implies \sum_{\rm poles} \operatorname{Res} f(z) = -\frac i{2\sqrt2} \frac{\log^2(1-b) - \log^2(1+b)}{\sqrt b}$$
so by Cauchy's residue theorem,
$$I(b) = \frac\pi{2\sqrt2} \frac{\log^2(1-b)-\log^2(1+b)}{\sqrt b} + \frac\pi{\sqrt{2b}} \int_0^b \frac{\log(b-y)-\log(y)}{\sqrt y(1-y^2)} \, dy$$
As we let $b$ approach $1$ from below, on the left side we'll recover $I(1)=-2\,\mathcal I$. On the right side, $\sqrt b\to1$ and $\log^2(1+b)\to\log^2(2)$. The second integral converges to
$$\begin{align*} \int_0^1 \frac{\log(x)}{\sqrt x (1-x^2)} \, dx &= 4 \int_0^1 \frac{\log(x)}{1-x^4} \, dx \\[1ex] &= -4 \sum_{n=0}^\infty \int_0^1 x^{4n} \log(x) \, dx \\[1ex] &= -\sum_{n=0}^\infty \frac4{(4n+1)^2} \\[1ex] &= -2G - \frac{\pi^2}4 \end{align*}$$
where $G$ is Catalan's constant. Evaluating the sum follows from observing that $\frac1{(4n+1)^2}=\frac1{(2(2n)+1)^2}$. We subsequently find
$$\sum_{n\ge0} \frac1{(4n+1)^2} = \frac12 \sum_{k\ge0} \frac{(-1)^k+1}{(2k+1)^2} = \frac G2 + \frac{\pi^2}{16}$$
Solving for our integral, we have
$$\mathcal I = -\frac\pi{4\sqrt2} \left(4G+\frac{\pi^2}2-\log^2(2) + \underbrace{\lim_{b\to1^-} \left[\log^2(1-b) + 2 \int_0^b \frac{\log(b-y)}{\sqrt y(1-y^2)} \, dy\right]}_L\right)$$
By the fundamental theorem of calculus,
$$\log^2(1-b) = -2 \int_{1-b}^1 \frac{\log(x)}x \, dx = -2 \int_0^b \frac{\log(1-x)}{1-x} \, dx$$
Then in our limit, we have
$$\begin{align*} L &= \lim_{b\to1^-} \left[\log^2(1-b) + 2 \int_0^b \frac{\log(b-x)}{\sqrt x(1-x^2)} \, dx\right] \\[1ex] &= 2 \lim_{b\to1^-} \left[\int_0^b \frac{\log(b-x)}{\sqrt x (1-x^2)} \, dx - \int_0^b \frac{\log(1-x)}{1-x} \, dx\right] \\[1ex] &= 2 \int_0^1 \frac{\log(1-x) - \sqrt x(1+x)\log(1-x)}{\sqrt x (1-x^2)} \, dx \\[1ex] &= 4 \int_0^1 \frac{1-x-x^3}{1-x^4} \log(1-x^2) \, dx \end{align*}$$
but there's still something wrong going on because $L$ isn't finite ...
For now, we arrive at the (still incorrect!) value
$$\implies \mathcal I = - \frac{\pi^3}{8\sqrt2} - \frac\pi{\sqrt2}G + \frac\pi{4\sqrt2} \log^2(2) - \frac\pi{4\sqrt2} L$$
so it remains to find out why the integral in $L$ isn't playing nice. (In an earlier edit, the constant term in the numerator was $2$ instead of $1$ which was enough for convergence.)
$$\mathcal I = -\frac{\pi^3}{12\sqrt2} -\frac\pi{\sqrt2} G -\frac{3\pi}{4\sqrt2}\log^2(2) - \frac{\pi^2}{4\sqrt2}\log(2)$$
$ \displaystyle \int _{ 0 }^{ \pi /2 }{ x\sqrt { \tan { (x) } } \log { (\cos { (x) } ) } dx }=-\frac{\pi\sqrt{2}}{8}(\frac{\pi^2}{3}+4G+3\ln^22+{\pi}{\ln{2}}) $
