2

enter image description here

Premise 1: Line is composed of points.
Premise 2: Each point is associated with specific co-ordinates (x,y).
Premise 3: Lines of equal length have equal number of points. Lines of greater length have greater number of points.
Premise 4: Each value of x in the function f(x) gives a single value of y.
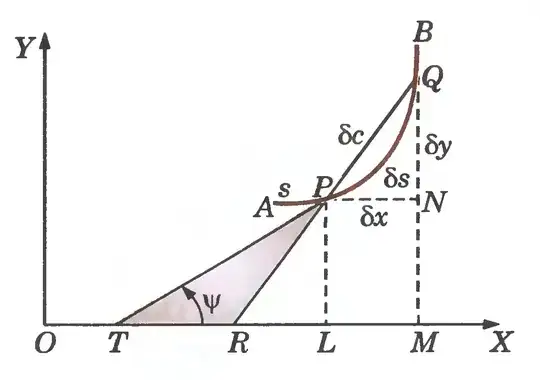
Premise 5: Each point (x,0) between L and M is associated with a unique point of (x,y) according to the function y = f(x). So, each point on the length LM has a unique single partner on the arc PQ. Hence, number of points on the arc is equal to number of points on the line LM. Length LM = Length of arc PQ.

Conclusion: The above analysis seems to conclude length of LM to be equal to length of arc PQ, which is definitely wrong as evident from the figure itself.

So, is length of arc PQ greater than LM?

The figure has been extracted from the book "Higher Engineering Mathematics" by Dr.B.S.Grewal.

Sensebe
  • 915
  • Yeah, and, paradoxically [0,1] and [0,2] has the same number of points. Proof: there is a one-to-one relationship between the point so the two intervals. Measure and cardinality are different things. – zoli Mar 06 '15 at 14:09
  • 1
    The second half of Premise 3 is false. – TonyK Mar 06 '15 at 14:09
  • @TonyK: Can you suggest some layman books on this matter? – Sensebe Mar 06 '15 at 14:36
  • 1
    @Feynman: You might like to look at this MSE question and the answer I gave there. It is perhaps not for the layperson, but it gives you an idea of the kind of arguments used to evaluate arc lengths. – TonyK Mar 06 '15 at 14:43
  • $y=2x$ maps uniquely $[0,1]$ to $[0,2]$; point by point... – zoli Mar 06 '15 at 16:24

2 Answers2

3

What is wrong is one of your premises:

Premise 3: Lines of equal length have equal number of points. Lines of greater length have greater number of points.

When a set has infinitely many number of points, you cannot compare them this way. For example, the number of rational numbers is "equal to" the number of natural numbers. This number is called the cardinality of the sets.

Think about this: Any line segment can be mapped to another line segment in a way such that each point on one is associated with a point on the other.

KittyL
  • 16,965
0

No, the number of points being infinite, it bears no relation to the length. Actually, it doesn't measure anything, as "$\infty=\lambda\infty$".