How do we define arc length?

Question

In trying to write a nice proof of the derivatives of $\sin(x)$ and $\cos(x)$, I encountered a serious problem, namely that I have never seen a proper definition of the notion of arc length. Based on visual intuition (for whatever that means), I tried to argue as follows:

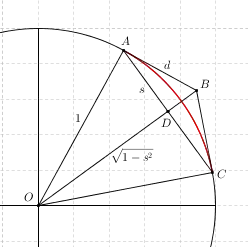
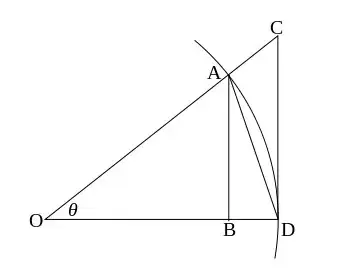
Consider the following diagram:

The chord $AC$ is shorter than the red arc which is again (by visual intuition) shorter than the path $ABC$. This means that $$2s<arc<2d$$ Note that $|OD|=\sqrt{1-s^2}$ by the Pythagorean theorem. Now, since $\Delta ABD$ and $\Delta OAD$ are similar, we see that $$\frac sd=\frac{\sqrt{1-s^2}}1$$ so dividing the chord length $2s$ by $2s,arc$ and $2d$ considering inequalities from before we then have $$1>\frac{2s}{arc}>\frac{2s}{2d}=\sqrt{1-s^2}$$ and it follows that $$\frac{2s}{arc}=\frac{chord}{arc}\longrightarrow 1\quad\text{when}\quad chord,arc\longrightarrow 0$$

Problem: Since the inequality $arc<2d$ was based solely on intuition, I could just as well have claimed that $\frac{chord}{arc}\longrightarrow 1$ by intuition in the first place anyway. Perhaps my intution about the inequality is stronger than my intuition about the limit, but that does not make it more rigorous ...

Question: How can we define the notion of arc length and based on that show rigorously that $arc<2d$?

Answer 1

One way to define the arc length of a curve $\gamma:[a,b]\to\mathbb R^2$ is by considering partitions of $[a,b]$, as in Riemann integration (read this Wikipedia article first): if $P(x,t)$ is a tagged partition of $[a,b]$, then $L_\gamma(P)$, the length of $\gamma$ with respect to the partition $P$, is $\sum_{i=1}^{n-1}|\gamma(t_i)-\gamma(t_{i-1})|$.

Definition: If $\underset{P}{\lim \sup} L_\gamma(P)$ exists, then $L_\gamma = \underset{P}{\lim \sup} L_\gamma(P)$ is the length of the curve.

Now consider the portion of the red arc between the point $A$ and the line $BD$. Using the above definition, we can see that the length of this arc lies between $AD$ and $AB$: if $\gamma(t_{i-1})$ and $\gamma(t_i)$ are points on the curve, we can project them perpendicular to $AD$ onto the points $r_{i-1}$ and $r_i$ on $AD$, and $s_{i-1}$ and $s_i$ on $AB$. And then we have $|r_i-r_{i-1}| < |\gamma(t_i)-\gamma(t_{i-1})| < |s_i-s_{i-1}|$, by simple geometry.

Therefore $L_{AD}(P) < L_\gamma(P) < L_{AB}(P)$ (taking some liberties with the notation). And in the limit we get:

$$\underset{P}{\lim \sup}L_{AD} \le \underset{P}{\lim \sup}L_\gamma(P) \le \underset{P}{\lim \sup}L_{AB}$$

In other words: $$AD \le L_\gamma\le AB$$

To show strict inequality would not be too difficult $-$ for instance, if we are more than halfway to the line $BD$, then there is a constant $\mu < 1$ such that $|\gamma(t_i)-\gamma(t_{i-1})| < \mu|s_i-s_{i-1}|$. This would give $L_\gamma(P) < \frac12(1+\mu)L_{AB}(P)$, so $L_\gamma \le \frac12(1+\mu)AB$.

Answer 2

Given an injective, piecewise $C^1$ parameterization $r(t)$, $t \in [a, b]$ of a curve $\gamma$, we can define the arc length element to be $$ds := \left\vert r'(t)\right\vert \,dt,$$ and correspondingly the (arc) length of $\gamma$ to be $$L(\gamma) = \int_{\gamma} ds = \int_a^b \left\vert r'(t)\right\vert \,dt.$$

Critically, the arc length element $ds$ and the length $L(\gamma)$ does not depend of the choice of parameterization $r(t)$. Indeed, we can write any other such parameterization of $\gamma$ as $r(t(\tau))$ for some monotonic function $t(\tau)$, and independence of parameterization follows immediately from applying the chain rule to the change of variable $t \mapsto \tau$.

Note that we can parameterize the graph of a function $f(x)$, $x \in [a, b]$, by the curve $r(t) = \langle t, f(t)\rangle$, $t \in [a, b]$, in which case the arc length element is $\left\vert r'(t)\right\vert = \left\vert\langle1, f'(t)\rangle\right\vert = \sqrt{1 + f'(t)^2}$, which leads immediately to the formula given in mvw's answer for the arc length of such a curve.

Answer 3

another method to deduce derivatives of trig functions
(Not an answer to the original question, since it does not involve arc length. But the original question shows that the "arc length" approach may not be so intuitively obvious. Thus, my preference for an "area" method.) (Found in many textbooks, and, for example, http://en.wikipedia.org/wiki/Proofs_of_trigonometric_identities#Inequalities).

We consider angle $\theta > 0$, but close to zero. Similar diagrams may be made for $\theta<0$. Let angle $\theta$ be given. Draw a unit circle with center $O$. Let radii $OD$ and $OA$ of that circle be such that $\angle AOD = \theta$.

Let point $B$ be on segment $OD$ so that $AB$ is perpendicular to $OD$. Let $C$ be on ray $OA$ such that $DC$ is perpendicular to $OD$. Thus $DC$ is tangent to the circle. According to trigonometry, $|OB| = \cos \theta$, $|AB| = \sin \theta$, $|CD| = \tan \theta$.

Now, when $\theta \to 0+$, point $B$ approaches point $D$, so we get a cosine limit $$ \lim_{\theta\to 0+}\cos\theta = 1 $$

Now consider the sector of the circle between the two radii $OA$ and $OD$. This sector is the fraction $\theta/(2\pi)$ of the whole circle. The whole circle has area $\pi$, so this sector has area $\pi \cdot \theta/(2\pi) = \theta/2$.
The triangle $OAD$ has area $|OD|\cdot|BA|/2 = (\sin\theta) / 2$. This triangle is contained in the sector, so the area of the triangle is less than the area of the sector. So we get inequality $$ \sin\theta < \theta $$

The triangle $ODC$ has area $|OD|\cdot|CD|/2 = (\tan \theta) / 2$. This triangle contains the sector, so we get inequality $$ \theta < \tan \theta = \frac{\sin\theta}{\cos\theta} $$

Now, from these inequalities, we get $$ \cos\theta < \frac{\sin\theta}{\theta} < 1 $$ Using the cosine limit above, we have a sine limit: $$ \lim_{\theta \to 0+}\frac{\sin\theta}{\theta} = 1 $$

Now we need another cosine limit. $$ \frac{1-\cos\theta}{\theta^2} = \frac{1-\cos^2\theta}{\theta^2(1+\cos\theta)} =\frac{\sin^2\theta}{\theta^2(1+\cos\theta))} = \frac{\sin\theta}{\theta} \cdot \frac{\sin\theta}{\theta}\cdot \frac{1}{1+\cos\theta} \to \frac{1}{2} $$ as $\theta \to 0$.

From these we can prove the formulas for the derivatives of the trig functions.

Answer 4

The differential arclength is $ds^2 = dx^2 + dy^2$. You can use this with the curve $y = y(x)$ of the arc and integration.

For a curve $y(x)$ over $x \in [x_1, x_2]$ the arc length of that curve is $$ s = \int\limits_{x_1}^{x_2} \sqrt{1+(y')^2}\,dx \quad (*) $$ Example The curve for a circle of radius $r$ and center at the origin is $$ y = \sqrt{r^2 - x^2} \quad y' = -\frac{x}{\sqrt{r^2 - x^2}} $$ so for the quarter circle in the first quadrant we have $$ s = \int\limits_0^r \frac{dx}{\sqrt{1-\left(\frac{x}{r}\right)^2}} = \left[r \arcsin\left(\frac{x}{r}\right)\right]_0^r = r \arcsin\left(1\right) = r\frac{\pi}{2} $$ which seems ok, a quarter of $2\pi r$.

Answer 5

This is not actually an answer, but some details that I left out in the original post to avoid it being too lengthy:

---

Once I have sorted out the problem of defining arc lengths and proven that $\frac{chord}{arc}\longrightarrow 1$ as $chord,arc$ tends to zero, my proof of the derivatives of $\sin(x)$ and $\cos(x)$ goes as follows:

For some fixed $x_0\in\mathbb R$ and variable $h\in\mathbb R$ define $$\vec v_0=\begin{pmatrix}\cos(x_0)\\\sin(x_0)\end{pmatrix}\quad\text{and}\quad\vec v=\begin{pmatrix}\cos(x_0+h)\\\sin(x_0+h)\end{pmatrix}$$ Then define the chord vector $\overrightarrow{\Delta v}=\vec v-\vec v_0$ and consider the following: $$\begin{pmatrix}\frac{\cos(x_0+h)-\cos(x_0)}h\\\frac{\sin(x_0+h)-\sin(x_0)}h\end{pmatrix}=\frac 1h\cdot\overrightarrow{\Delta v}=\underbrace{\frac{|\overrightarrow{\Delta v}|}{h}}_{chord/arc}\cdot\overbrace{\frac 1{|\overrightarrow{\Delta v}|}\cdot\overrightarrow{\Delta v}}^{\text{secant unit vector}}$$ Now, the first fraction is essentially $\frac{chord}{arc}$ tending to $1$ as $arc=h$ tends to zero. The rest is a secant unit vector through the endpoints of $\vec v$ and $\vec v_0$ respectively, so as $h$ tends to zero this tends to the tangent unit vector $$\widehat{\vec v_0}=\begin{pmatrix}-\sin(x_0)\\\cos(x_0)\end{pmatrix}$$ So we have shown that $$\begin{pmatrix}\frac{\cos(x_0+h)-\cos(x_0)}h\\\frac{\sin(x_0+h)-\sin(x_0)}h\end{pmatrix}\longrightarrow\begin{pmatrix}-\sin(x_0)\\\cos(x_0)\end{pmatrix}$$ as $h$ tends to zero. Thus $\cos'(x_0)=-\sin(x_0)$ and $\sin'(x_0)=\cos(x_0)$.

Answer 6

I think there are many ways to define an arc length (especially of a circle)

For a circle the arclength is:

• The length of the perimeter of the inscribed regular polygon as the number of vertices grows to $ \infty$ (compare s)

• The length of the perimeter of the circumscribed regular polygon as the number of vertices grows to $\infty$ (compare d)

• How about taking half of the sums above?