(This is a short version of the question intended to post, because the original is just TOO LONG)
From this link and various others (including 2 links deleted by the system as part of the clean up process, unfortunately...) we learnt how to manipulate partial derivatives rigorously.
We have learnt in undergraduate on how to write chain rules of multivariable functions using chain rule diagrams such as this one (variables that are kept constant are shown explicitly because the function is written in full)
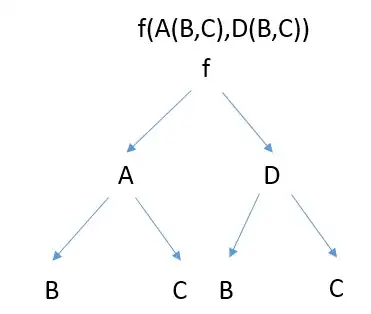
$$\frac{\partial f(A(B,C),D(B,C)) )}{\partial B}=\frac{\partial f(A(B,C),D(B,C))}{\partial A(B,C)}\frac{\partial A(B,C)}{\partial B}+\frac{\partial f(A(B,C),D(B,C))}{\partial D(B,C)}\frac{\partial D(B,C)}{\partial B}$$
Or using another notation according to the link
$$\left.\frac{\partial f}{\partial B}\right|_C=\left.\frac{\partial f}{\partial A}\right|_D\left.\frac{\partial A}{\partial B}\right|_C+\left.\frac{\partial f}{\partial D}\right|_A\left.\frac{\partial D}{\partial B}\right|_C$$
Things looks fine. However when you have a function that look something like this
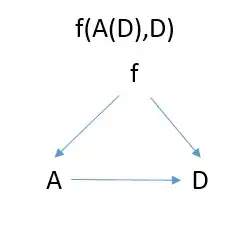
Attempt to write a chain rule gives a bizarre result for at least one of the variables
$$\left.\frac{\partial f}{\partial A}\right|_D$$ $$\color{red}{\left.\frac{\partial f}{\partial D}\right|_{A?}}=\left.\frac{\partial f}{\partial A}\right|_{D?}\frac{dA}{dD}+\color{red}{\left.\frac{\partial f}{\partial D}\right|_{A?}} \hspace{12 mm} [*]$$
If we consider the red terms identical, then we get $$0=\left.\frac{\partial f}{\partial A}\right|_{D?}\frac{dA}{dD}$$
Why the bizarre result? How to interpret or explain it (both geometrically and mathematically?)