4

enter image description here

Start with

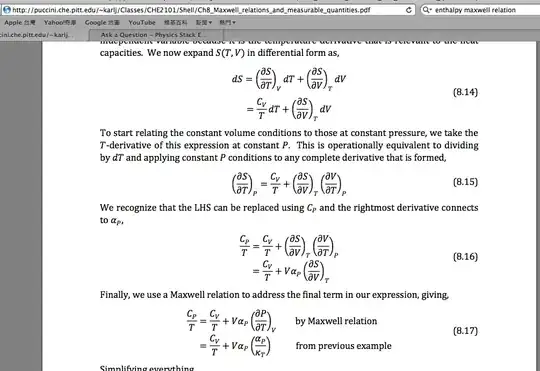
$$dS=\left(\frac{\partial S}{\partial T}\right)_VdT+\left(\frac{\partial S}{\partial V}\right)_TdV$$

Using the notes shown here

Method 1:

i) Divide both sides by dV $$\frac{dS}{dV}=\left(\frac{\partial S}{\partial T}\right)_V\frac{dT}{dV}+\left(\frac{\partial S}{\partial V}\right)_T\frac{dV}{dV}$$

ii) and at const. P

$$\left(\frac{dS}{dV}\right)_P=\left(\frac{\partial S}{\partial T}\right)_V\left(\frac{dT}{dV}\right)_P+\left(\frac{\partial S}{\partial V}\right)_T\left(\frac{dV}{dV}\right)_P$$

$$\left(\frac{dS}{dV}\right)_P=\left(\frac{\partial S}{\partial T}\right)_V\left(\frac{dT}{dV}\right)_P+\left(\frac{\partial S}{\partial V}\right)_T$$

Question 1: but how does

$$\left(\frac{dS}{dV}\right)_P=\left(\frac{\partial S}{\partial T}\right)_V\left(\frac{dT}{dV}\right)_P+\left(\frac{\partial S}{\partial V}\right)_T$$

becomes

$$\left(\frac{\partial S}{\partial V}\right)_P=\left(\frac{\partial S}{\partial T}\right)_V\left(\frac{\partial T}{\partial V}\right)_P+\left(\frac{\partial S}{\partial V}\right)_T???$$

Using the notes shown here

Method 2:

Differentiate both side wrt V, holding P const. and use product rule

$$\frac{\partial}{\partial V}\left(dS\right)_P=\frac{\partial}{\partial V}\left(\left(\frac{\partial S}{\partial T}\right)_VdT\right)_P+\frac{\partial}{\partial V}\left(\left(\frac{\partial S}{\partial V}\right)_TdV\right)_P$$

$$\left(\frac{\partial dS}{\partial V}\right)_P=\left(\left(\frac{\partial^2 S}{\partial V \partial T}\right)_V\right)_PdT+\left(\frac{\partial S}{\partial T}\right)_V\left(\frac{\partial dT}{\partial V}\right)_P+\left(\left(\frac{\partial^2 S}{\partial V^2}\right)_T\right)_PdV+\left(\frac{\partial S}{\partial V}\right)_T\left(\frac{\partial dV}{\partial V}\right)_P$$

Question 2: I got so many extra terms, and how to deal with these $$\left(\frac{\partial \text{ d blah}_1}{\partial \text{ blah}_2}\right)_{\text{blah}_3}$$ terms?

Tl:dr

How to partial differentiate a total differential rigorously?

Community
  • 1
Secret
  • 2,390

1 Answers1

0

A few rules : be clear as to what the independent variables are, use the chain rule, specify precisely which variables are kept constant while taking the partial derivative, and never operate on partial derivatives formally (e.g. "cancelling".

Take the entropy, S. It is a function of two independent variables, T and V. What do we mean when we say that? One way of looking at it is that changing either T or V can lead to a change in the value of S. If you imagine T and V on the x and y axes, S=S(T,V) defines a surface in space. The partial derivatives $$ \left. \frac{\partial S}{\partial T} \right|_{V} \quad, \quad \left. \frac{\partial S}{\partial V} \right|_{T} $$ (respectively) tell you about the rate of change of S with respect to T keeping V constant and the rate of change of S with respect to V keeping T constant.

If you varied $T$ by a small amount $dT$ and kept $V$ unchanged, S would change by an amount $\left. \frac{\partial S}{\partial T} \right|_{V} dT$. You can write something similar for a small change $dV$ in V while keeping $T$ constant.

The total change in the variable $S$ is then $$ dS = \left. \frac{\partial S}{\partial T} \right|_{V} dT + \left. \frac{\partial S}{\partial V} \right|_{T} dV $$

Now consider a third variable P. Clearly, you can write $P=P(V,T)$ since two independent variables suffice to characterize the state of the system. The relation between P,V and T can sometimes be an explicit relation, like the ideal gas law $PV=nRT$. So now one can replace the V dependence of S by a P dependence using this relation. [Specify any two of P, V and T and the third one is known.]

We now write

$$ S=S(T,V)=S(T,V(P,T)) $$

Now apply the chain rule to find $dS$ in this instance. We write the outer dependencies first and then expand till we have only independent variables (P and T) in the expression. In steps,

$$ S=S(T,V(P,T)) \\ \Rightarrow dS = \left. \frac{\partial S}{\partial T} \right|_{V} dT + \left. \frac{\partial S}{\partial V} \right|_{T} dV $$ But dV itself is now produced by changes to T and P, so you have to expand it as follows: $$ dV = \left. \frac{\partial V}{\partial T} \right|_{P} dT + \left. \frac{\partial V}{\partial P} \right|_{T} dP $$ to give you $$ dS = \left. \frac{\partial S}{\partial T} \right|_{V} dT + \left. \frac{\partial S}{\partial V} \right|_{T} \left( \left. \frac{\partial V}{\partial T} \right|_{P} dT + \left. \frac{\partial V}{\partial P} \right|_{T} dP \right) $$ Gathering terms in dT and dP, $$ dS = \left( \left. \frac{\partial S}{\partial T} \right|_{V} + \left. \frac{\partial S}{\partial V} \right|_{T} \left. \frac{\partial V}{\partial T} \right|_{P} \right) dT + \left. \frac{\partial V}{\partial P} \right|_{T} dP $$

Now, the LHS of Eq. 8.15 has $\left. \frac{\partial S}{\partial T} \right|_{P}$. This is a rate of change of S with respect to T while allowing no change in the pressure, i.e. dP=0. Note that any derivative you write is a partial derivative if you suppress change in one or more variables.

You have

$$ \left. \frac{\partial S}{\partial T} \right|_{P} = \left. \frac{\partial S}{\partial T} \right|_{V} + \left. \frac{\partial S}{\partial V} \right|_{T} \left. \frac{\partial V}{\partial T} \right|_{P} $$

You can show that $c_v / T = \left. \frac{\partial S}{\partial T} \right|_{V}$, so you finally have

$$ \left. \frac{\partial S}{\partial T} \right|_{P} = \frac{c_v}{T} + \left. \frac{\partial S}{\partial V} \right|_{T} \left. \frac{\partial V}{\partial T} \right|_{P} $$

user_of_math
  • 4,192
  • So to go from $$ dS = \left( \left. \frac{\partial S}{\partial T} \right|{V} + \left. \frac{\partial S}{\partial V} \right|{T} \left. \frac{\partial V}{\partial T} \right|{P} \right) dT + \left. \frac{\partial V}{\partial P} \right|{T} dP $$

    to

    $$ \left. \frac{\partial S}{\partial T} \right|{P} = \left. \frac{\partial S}{\partial T} \right|{V} + \left. \frac{\partial S}{\partial V} \right|{T} \left. \frac{\partial V}{\partial T} \right|{P} $$

    We are not actually differentiating wrt dT keeping P constant but, just recognizing that the (.) in the (.)dT term is

     – Secret Nov 26 '14 at 09:05
  • $\left. \frac{\partial S}{\partial T} \right|_{P}$ ?

    which physicists often said as dividing by dT and let P constant is because the notations in the expression look superficially the same, but what actually happening is $\left. \frac{\partial S}{\partial T} \right|_{P}$ term is another expression that forms part of dS?

     – Secret Nov 26 '14 at 09:05
  • @Secret Yes. Once you know $dS = ()dT + ()dP$ it follows from the definition of the partial derivative that the first () contains $\left. \frac{\partial S}{\partial T} \right |_P$. The notion of "dividing by dT" is a bit misleading and unnecessary. – user_of_math Nov 26 '14 at 09:50
  • Btw, for part 2, is a total differential of a function (e.g. dS) is not a function itself (only S is), thus we never partial differentiate any d(blah) terms? – Secret Nov 26 '14 at 11:26
  • @Secret Yes, you could think of it that way. You should never have to take partial derivatives of d(whatever) by itself, only of (whatever) keeping some variable fixed. – user_of_math Nov 26 '14 at 11:33