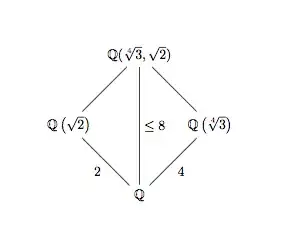
I want to show that $\sqrt{2}\notin \mathbb{Q}(\sqrt[4]{3})$.
I think it would be easier to prove it using the following: $\mathbb{Q}\subset\mathbb{Q}(\sqrt{3})\subset\mathbb{Q}(\sqrt[4]{3})$. Then $\sqrt{2}\notin\mathbb{Q}(\sqrt{3})$ so $\sqrt{2}\in \mathbb{Q}(\sqrt[4]{3})\Longleftrightarrow \sqrt{2}=a+b\sqrt[4]{3}$, with $a,b\in\mathbb{Q}(\sqrt{3})$.
I tried simplifying the above equation, but I did not get anything.
If we had $\sqrt{2}\in \mathbb{Q}(\sqrt[4]{3})$ we would deduce, since $\sqrt 3\in \mathbb{Q}(\sqrt[4]{3})$], that $\mathbb{Q}(\sqrt{2}, \sqrt 3)\subset \mathbb{Q}(\sqrt[4]{3})$ and thus for degrees reason that $\mathbb{Q}(\sqrt{2}, \sqrt 3)= \mathbb{Q}(\sqrt[4]{3})$.
But this is impossible because $\mathbb{Q}(\sqrt{2}, \sqrt 3)$ is normal over $\mathbb Q$ as the splitting field of $(X^2-2)(X^2-3)$, while $\mathbb{Q}(\sqrt[4]{3})$ is not normal since it contains one but not all roots of the irreducible polynomial $X^4-3$.
As you have deduced it is easiest to consider $\mathbb{Q}(\sqrt[4]{3})$ as a vector space over $\mathbb{Q}(\sqrt{3})$. First one must check that $\sqrt{2}\notin\mathbb{Q}(\sqrt{3})$, which I will not do here. Then we must deduce that there is no element $a+b\sqrt[4]{3}$ with $a,b\in\mathbb{Q}(\sqrt{3})$ that squares to $2$. Squaring we get $$(a^2+b^2\sqrt{3})+2ab\sqrt[4]{3}$$ If this is equal to $2$ then $2ab\sqrt[4]{3}=0$, which implies either $a=0$ or $b=0$. Since $\sqrt{2}\notin\mathbb{Q}(\sqrt{3})$, $b$ cannot be $0$, hence $a$ must be $0$. In that case we have $$b^2\sqrt{3}=2$$ so $$b^2=\frac{2}{3}\sqrt{3}$$ Since $b=x+y\sqrt{3}$ for some $x,y\in\mathbb{Q}$ we have $$x^2+3y^2+2xy\sqrt{3}=\frac{2}{3}\sqrt{3}$$ or $$x^2+3y^2=(\frac{2}{3}-2xy)\sqrt{3}$$ However the left side is rational and the right side is irrational unless it is $0$, hence we have a contradiction.
It is enough to show $\sqrt[4]{3} \not \in \mathbb{Q}(\sqrt{2})$. Why?
$\sqrt[4]{3} = a+b\sqrt{2} \Rightarrow \sqrt{3} = a^2+2\sqrt{2}ab+2b^2 \Rightarrow \frac{\sqrt{3}}{2ab}-\frac{a^2+2b^2}{2ab}=\sqrt{2} \Rightarrow \sqrt{2} \in \mathbb{Q}(\sqrt{3})$.
If you haven't proven this already, observe that if $\sqrt{2}=c+d\sqrt{3}$ then we have the following,
$2=(c^2+3d^2)+(2cd\sqrt{3}) \Rightarrow c=d=0$ since if not we would have $\sqrt{3} \in \mathbb{Q}$.
One method is to just take a brute force approach. Let $x = \sqrt[4]{3}$ so that $\{1, x, x^2, x^3\}$ is a basis for $\mathbb Q(\sqrt[4]{3})$ over $\mathbb Q$. Then write $$\sqrt{2} = a + bx + cx^2 + dx^3.$$ Square this and reduce using the relation $x^4 = 3$, then equate basis coefficients and show that the resulting system of equations has no solution.
