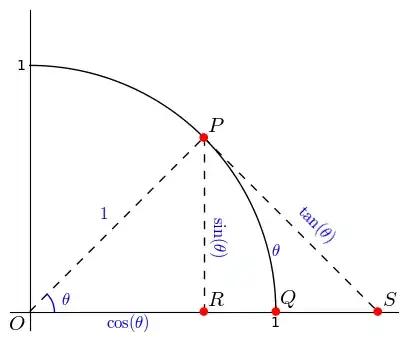
Prove that $\sin x0$

Question

Prove that $\sin x<x$, if $x>0$.

May it seems a silly question, but I don't know how to prove it analytically (i.e., without comparing graph of $\sin x$ and $x$) and without more advanced topics, e.g. Taylor series, or even derivation.

Please help me how can I prove it for a middle-school student, using definition of $\sin x$ or maybe some trigonometric identities.

Thank you.

@Mario Carneiro: Not duplicate; I know all the methods written in the link you mentioned, but I am trying to prove it geometrically for a pre-high-school. — , Feb 10 '15 at 10:26
Then middle-school methods should be added as another answer on that question. It would be better to have all the proofs in one place. — Mario Carneiro, Feb 10 '15 at 10:28
You can find this inequality also here: http://math.stackexchange.com/questions/390899/sinx-inequality It is also proved in some answers on questions about limits, such as http://math.stackexchange.com/questions/75130/how-to-prove-that-lim-limits-x-to0-frac-sin-xx-1 and http://math.stackexchange.com/questions/117548/i-want-to-prove-the-following-limit-lim-x-rightarrow-0-frac-sin-xx2 (And you could look also at some other posts listed on the right among related questions.) — Martin Sleziak, Feb 10 '15 at 11:37

score 10 · Accepted Answer · edited Feb 10 '15 at 10:31

10

Consider the unit circle. $\alpha$ is the length of the arc, while $\sin(\alpha)$ is the length of the orthogonal projection on the $x$-axis. For obvious reasons - a middle school student will believe you - the arc is longer.

diagram

edited Feb 10 '15 at 10:31

Mario Carneiro

27,438

answered Feb 10 '15 at 10:22

MooS

31,390

1

Add to it that one can assume $x<\pi/2$, because for $x\ge\pi/2$ the inequality is obvious. – egreg Feb 10 '15 at 10:31
2

I took the liberty of editing in a diagram, taken from http://math.stackexchange.com/a/75135/50776. (That question also includes many geometric proofs of $\sin x<x<\tan x$, since it is a lemma for $\sin x/x\to1$.) – Mario Carneiro Feb 10 '15 at 10:31
1

I would believe that already for $x>1$ the inequality is obvious. – Fabian Feb 10 '15 at 10:32
Yes of course, but that geometric argument works fine for $0<x<\frac{\pi}{2}$ and one should point that out. – MooS Feb 10 '15 at 10:33
@MarioCarneiro How did you draw that picture? – hola Mar 21 '15 at 10:45
@pushpen.paul Ask J.M., who edited in the diagram from the linked question. – Mario Carneiro Mar 21 '15 at 13:55

Prove that $\sin x0$

1 Answers1

Linked