pdf of a quotient of uniform random variables

Question

Suppose $x_1, x_2$ are IDD random variables uniformly distributed on the interval $(0,1)$. What is the pdf of the quotient $x_2 / x_1$?

Answer 1

Because $X_2$ is positive with almost surely, cumulative distribution function for $Z=X_1/X_2$ is $$ F_Z(z) = \mathbb{P}(Z \leqslant z) = \mathbb{P}(X_1 \leqslant z X_2) = \mathbb{E}_{X_2}\left( \mathbb{P}(X_1 \leqslant z X_2 | X_2)\right) = \mathbb{E}_{X_2}\left( F_{X_1}(z X_2)\right) $$ Clearly $F_Z(z)=0$ for $z\leqslant 0$, so assume $z > 0$ $$ F_Z(z) = \int_0^1 \left\{ \begin{array}{cl} z x_2 & 0 < x_2 <1/z \\ 1 & x_2 > 1/z \end{array} \right. \mathrm{d} x_2 = \frac{z}{2} \left(\frac{1}{\max(z,1)}\right)^2 + \left(1 - \frac{1}{\max(z,1)}\right) = \left\{\begin{array}{cl} \frac{z}{2} & 0< z\leqslant 1 \\ 1-\frac{1}{2z} & z > 1 \end{array} \right. $$ The probability density is obtained by differentiation.

Answer 2

Late to the party, but I want to have one post on SE that addresses this question in its raw formulation (no secondary issues or finer points in many similar questions), and taking advantage of the comment to the accepted answer about using triangles.

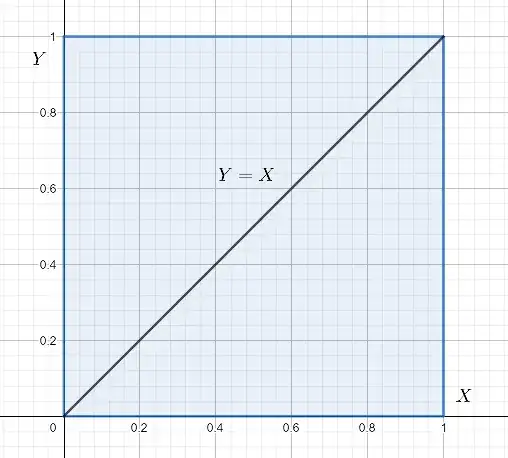
Renaming the rv's, $X$ and $Y$ as iid uniform distributions $X,Y \sim U[0,1],$ and the ratio $Z=Y/X,$ there are a few arithmetical and geometrical observations that suffice to derive both the pdf and cdf:

First off, the ratio can't be negative, since both $X$ and $Y$ are positive.

Second, observing the support of $Z$ in the Cartesian plane it is clear that it forms a square of area $1$ with a uniform distribution $f_{XY}(x,y)=1.$

Realizations of the rv $z=1$ will fall along the line $X=zY=Y$ corresponding to a slope of $1:$

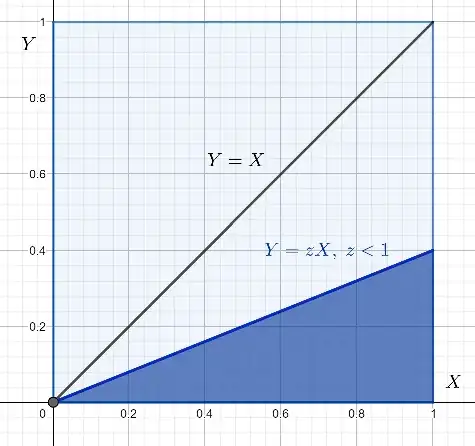
If $0\leq Z\leq 1,$ the intersection of the line with the right boundary of the square domain will be $(1,z),$ i.e. the slope of the line $(Z):$

The area in dark blue will be (given the independence and uniformity of $X$ and $Y)$ the probability $\Pr(Y/X\leq z)= \Pr(Y \leq zX)= \frac1 2 z.$

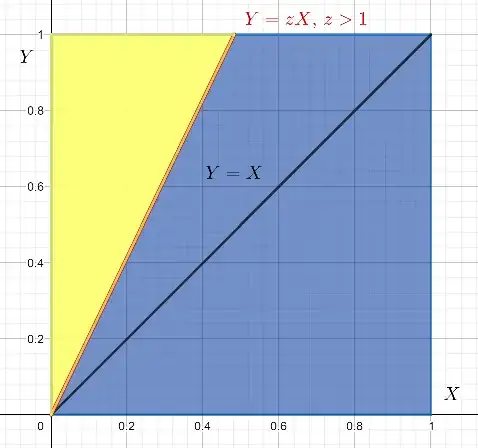
If, on the other hand, $z>1,$ the line will intersect the top margin of the square, at precisely $x = 1/z.$ The area below the line will be cumbersome to directly calculate, and it is hence much easier to get the complementary (yellow triangle):

as $\Pr(Y/X \leq z)=1 -\color{tan}\triangle=1 - \frac 1 {2z}$

Wrapping it up, then, the cdf is

F_Z(z) = \begin{cases} z/2, & 0 \le z \leq 1 \\ 1-\frac 1{2z}, & \text{if } z > 1 \\ 0, & \text{otherwise}. \end{cases}

And differentiating, the pdf is

f_Z(z) = \begin{cases} 1/2, & 0 \le z \leq 1 \\ 1-\frac 1{2z^2}, & \text{if } z > 1 \\ 0, & \text{otherwise}. \end{cases}