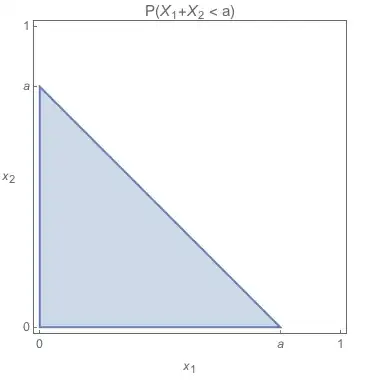
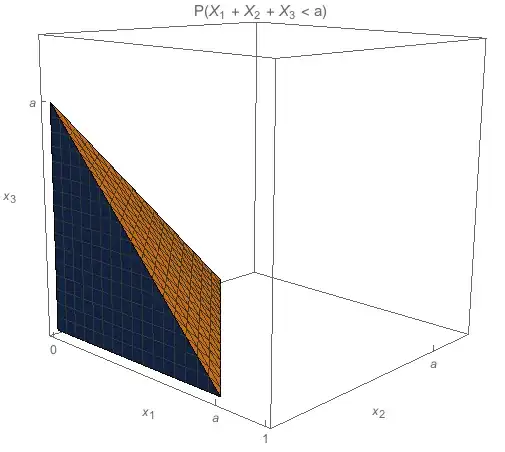
Let $\{X_r : r\ge 1\}$ be independently and uniformly distributed on $[0,1]$. Let $0<x<1$ and define
$$N=\min\{n\ge 1 : X_1 + X_2 +\ldots+X_n> x\}$$
Show that $$P(N>n) = \frac{x^n}{n!}$$ and hence find the mean and variance of $N$.
I cant see how $N$ can be greater than $n$, as each $X_r$ is less than or equal $1$, so if each $X_r= 1$, then the sum would equal $n$, but not be greater. I am obviously interpreting this wrong but I cant see where.