2

Accoring to Wolfram|Alpha, Georges Graph

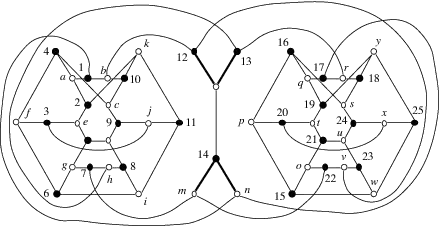
$\hskip1in$ enter image description here

is 3-edge colorable. Does anybody have a actual 3-edge coloring in form of three sub-matrices of the adjacence matrix: $$A_1+A_2+A_3=A $$

I tried to get them along the lines given here without success...

EDIT: Some further properties of Georges Graph are:

asymmetric | bicolorable | biconnected | bicubic | bipartite | bridgeless | class 1 | connected | cubic | cyclic | local | noncayley | noneulerian | nonhamiltonian | nonplanar | perfect | perfect matching | regular | square-free | traceable | triangle-free | weakly regular

Maybe this helps someone to help me...

Community
  • 1
draks ...
  • 18,449

1 Answers1

1

Every 3 edge coloring of a graph will have the adjacency matrix property you seek. Let $c(uv)=i$, then $a_{uv}=1$ in $A_i$. In other words, the coloring induces a partition of the edges.

Laars Helenius
  • 7,965
  • 1
  • 23
  • 35
  • ...can you give an actual example for a coloring? – draks ... Jan 26 '15 at 23:03
  • Off the top of my head, no. But I would start by trying to find a spanning cycle, which you may or may not be able to do. If one exists, apply an alternating coloring to that cycle. The remaining edges should be able to colored the third color.

    Another strategy might be to look for a maximal matching and color it 1, then look for another maximal matching and color it 2, with the remaining edges colored 3.

     – Laars Helenius Jan 26 '15 at 23:17
  • If by spanning cycle you mean a Hamilton cycle, I can say the Georges graph doesn't have one. – draks ... Jan 26 '15 at 23:26
  • OK. Then go with my second strategy. Start finding maximal matchings. – Laars Helenius Jan 26 '15 at 23:27
  • Concerning your idea about matchings it might be helpful to know that Georges Grah is bipartite. Do you know how to use König's Theorem? – draks ... Jan 26 '15 at 23:28
  • Being bipartite doesn't help much in edge colorings. It certainly tells us that the graph is 2-colorable. – Laars Helenius Jan 26 '15 at 23:30
  • Königs Theorem isn't much help in finding a matching. It only tells us if a perfect matching exists, in a roundabout way. Plus being bipartite only tells us that G is 2-colorable. – Laars Helenius Jan 26 '15 at 23:32
  • Look, don't be afraid to spend some time with this and try some colorings. Sometimes the best thing to do is to make some hard copies of this graph and grab some markers! – Laars Helenius Jan 26 '15 at 23:33
  • Laars, believe me: I tried. Without success. That's why I ask. But not matchings, so I'll try this as well... – draks ... Jan 26 '15 at 23:37
  • There are many algorithms for finding maximum matchings in bipartite graphs (constructing M-augmenting paths, for example). I got many hits on Google, but I'm not sure which website has the best explanation. – Randy E Jan 27 '15 at 20:59
  • +1... but thanks for your effort anyway! – draks ... Jan 31 '18 at 15:09