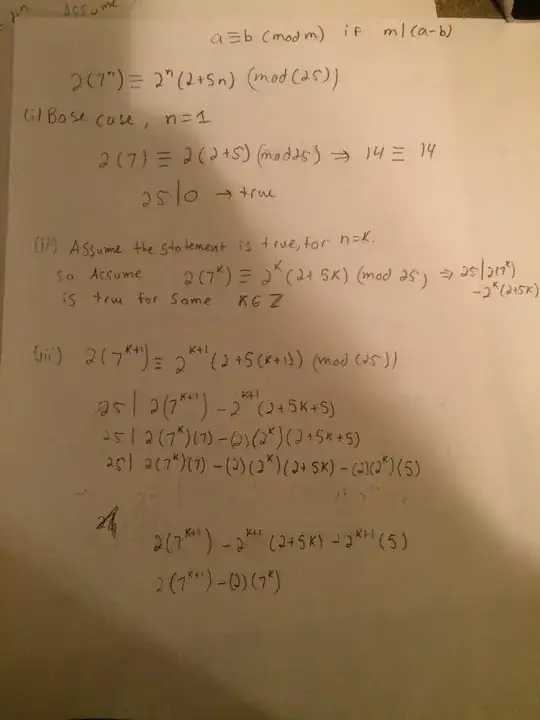$\underline{\text{Problem 1:}}$ For each positive integer $n$, let $M(n)$ be the statement that
$$
2\cdot 7^n \equiv 2^n\cdot(2+5n)\pmod{25}.
$$
Base step: $M(1)$ says that $14\equiv 14 \pmod{25}$, which is true.
Inductive step: Fix $k\geq 1$ and assume that
$$
M(k):\; 2\cdot 7^k \equiv 2^k\cdot(2+5k)\pmod{25}
$$
holds. It remains to show that
$$
M(k+1):\; 2\cdot 7^{k+1} \equiv 2^{k+1}\cdot(2+5(k+1))\pmod{25}
$$
follows. One can show this using just modular arithmetic; however, being a bit more pedantic, a few more steps may be added for clarity. Since $M(k)$ holds, we have the following:
$$
2\cdot 7^k \equiv 2^k\cdot(2+5k)\pmod{25} \Longleftrightarrow 2\cdot 7^k=2^k\cdot(2+5k) + 25\ell,
$$
where $\ell\in\mathbb{Z}$. Thus, we have the following:
\begin{align}
2\cdot 7^{k+1} &= (2\cdot 7^k)\cdot 7\\
&= (2^k\cdot(2+5k)+25\ell)\cdot 7\\
&= 7\cdot 2^k(2+5k)+7\cdot25\ell\\
&= 7\cdot 2^{k+1}+35k\cdot2^k+7\cdot 25\ell\\
&= 7\cdot 2^{k+1}+(25+2\cdot 5)k\cdot2^k+7\cdot 25\ell\\
&= 7\cdot 2^{k+1}+25k\cdot 2^k+5k\cdot2^{k+1}+7\cdot 25\ell\\
&= 2^{k+1}\cdot(7+5k)+25(7\ell+k\cdot2^k)\\
&\equiv 2^{k+1}\cdot(7+5k) \pmod{25}\\
&\equiv 2^{k+1}\cdot(2+5(k+1)) \pmod{25},
\end{align}
as desired, completing the proof of $M(k+1)$, and hence the inductive step. By mathematical induction, for each $n\geq 1$, the statement $M(n)$ holds.
$\underline{\text{Problem 2:}}$ Start by noting that we can use a strict inequality (i.e., $<$) here rather than $\leq$. Also note that
$$
\frac{(2n)!}{(n!)^2} < 4^n \Longleftrightarrow (2n)!<2^{2n}(n!)^2.
$$
There is nothing special about the equivalent expression on the right-hand side, but I find it to be a more natural expression to deal with; thus, I am going to prove this second problem with that expression in mind.
With that in mind, for each positive integer $n$, let $M(n)$ be the statement that
$$
(2n)!<2^{2n}(n!)^2.
$$
Base step: $M(1)$ says that $2<4$, which is true.
Inductive step: Fix $k\geq 1$ and assume that
$$
M(k):\;(2k)!<2^{2k}(k!)^2
$$
holds. It remains to show that
$$
M(k+1):\; [2(k+1)]!<2^{2(k+1)}[(k+1)!]^2
$$
follows. Beginning with the left side of $M(k+1)$,
\begin{align}
[2(k+1)]! &= (2k+2)!\\
&= (2k+2)(2k+1)(2k!)\\
&< (2k+2)(2k+1)[2^{2k}(k!)^2]\tag{ind. hyp.}\\
&< (2k+2)^2[2^{2k}(k!)^2]\tag{$2k+1 < 2k+2$}\\
&= [2(k+1)]^2\cdot[2^{2k}(k!)^2]\\
&= 2^2\cdot (k+1)^2\cdot 2^{2k}\cdot (k!)^2\\
&= 2^{2(k+1)}[(k+1)!]^2,
\end{align}
which is the right side of $M(k+1)$. By mathematical induction, for each $n\geq 1$, the statement $M(n)$ holds.