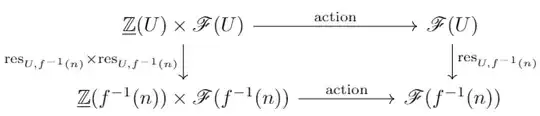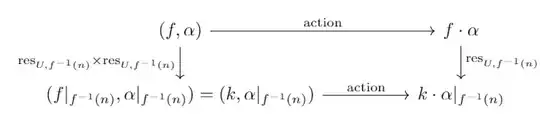Sheafs of abelian groups are the same as $\underline{\mathbb{Z}}$-modules

Question

In Vakil's notes page 76, he claims that a sheaf of abelian groups is the same as a $\underline{\mathbb{Z}}$-module, where $\underline{\mathbb{Z}}$ is the constant sheaf associated to $\mathbb{Z}$.

Let $F$ be a sheaf of abelian group over $X$. Given an open set $U\subset X$, we need to find an action

$$\underline{\mathbb{Z}}(U)\times F(U)\to F(U),$$ that is compatible with restriction. Recall that $$\underline{\mathbb{Z}}(U) = \{f: U\to \mathbb{Z}: \mathbb{Z} \text{ has discrete topology, $f$ continuous.}\}$$ So how does one define $f\times \alpha\mapsto ?$

I highly doubt the statement is correct. Idealy since an abelian group is a $\mathbb{Z}$-module, don't we want the constant presheaf asscoiated to $\mathbb{Z}$ rather than the constant sheaf?

Answer 1

I worked things out and have the following conclusion.

Abelian groups are the same as $\mathbb{Z}$-modules, therefore sheafs of abelian groups are the same as $\underline{\mathbb{Z}}^{pre}$-modules. However, due to the fact that sheafs have the identity and gluability property, this $\underline{\mathbb{Z}}^{pre}$ action can be canonically extended to a $\underline{\mathbb{Z}}$ action, the way @hoot described, where $\underline{\mathbb{Z}}^{pre}$ is identified as the constant functions inside $\underline{\mathbb{Z}}$.

This can also be explained from the adjunction of embedding and sheafification as @Zhen Lin described. The fact that the sheafification of the constant presheaf is the constant sheaf implies that a $\underline{\mathbb{Z}}^{pre}$-module extends uniquely to a $\underline{\mathbb{Z}}$-module.

Answer 2

For some reason this note of Vakil seemed to take a bit for me to unpack -- so once bumping into this question here I felt obligated to include what helped me eventually see the natural structure.

Let's take $\mathscr{F}$ to be a $\underline{\mathbb{Z}}$-module and $U$ some open set in $X$. As @Hoot indirectly mentioned through their comment, it is not hard to see $\mathcal{U}= \{f^{-1}(n)\}_{n\in\mathbb{Z}}$ forms an open cover -- and is arguably the best choice of a cover as $f$ is constant on each element. Since $\mathscr{F}$ is a $\underline{\mathbb{Z}}$-module, we have that for each $n \in \mathbb{Z}$ that

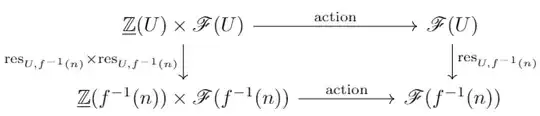
commutes, hence it follows that

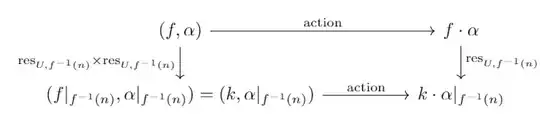
Using then the property that $\mathscr{F}$ is a sheaf, we can glue together each of the pieces of $f \cdot \alpha$ that are distributed throughout $\{\mathscr{F}(f^{-1}(n))\}_{n\in\mathbb{Z}}$ to get it back.

Neatly being stated: take $\mathcal{U}$ above to be our cover, $f_k = k \cdot \alpha|_{f^{-1}(k)} \in \mathscr{F}(f^{-1}(k))$, and note that for $n,m \in \mathbb{Z}$ that it should be clear we have \begin{align*} m=n &\implies f^{-1}(n) \cap f^{-1}(m) = f^{-1}(n) = f^{-1}(m) \\ m \neq n &\implies f^{-1}(n) \cap f^{-1}(m) = \emptyset \end{align*} thus in both case we trivially obtain that for all $n,m \in \mathbb{Z}$ $$\text{res}_{f^{-1}(n),f^{-1}(n) \cap f^{-1}(m)} f_n = \text{res}_{f^{-1}(n),f^{-1}(n) \cap f^{-1}(m)} f_m$$ (as recall that $\mathscr{F}(\emptyset)$ is a singleton). Hence by the conclusion of the gluability axiom, we can essentially "glue" our $f_i$'s all together to obtain an $F$ that restricts to each $f_i$ (i.e. we get the existence of such an $F$). The uniqueness of this $F$ follows from the identity axiom on $\mathscr{F}$. This resulting $F$ is what we then define to be $f\cdot \alpha$.