Is the usual proof of $\lim_{x\rightarrow 0}\frac {\sin(x)}{x} = 1$ an honest proof?

Question

In a lot of textbooks on Calculus a proof that $\lim_{x\rightarrow 0}\frac {\sin(x)}{x} = 1$ is the following:

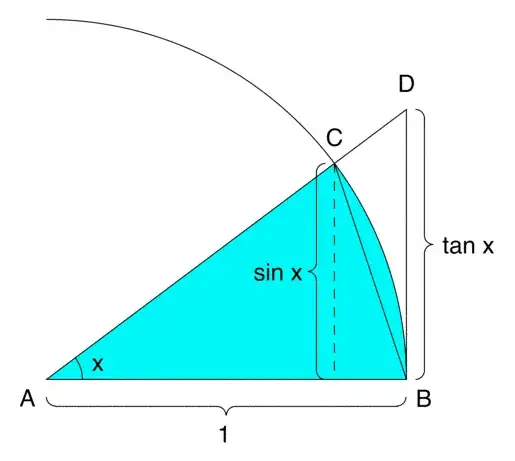
enter image description here

Comparing the areas of triangles $ABC, ABD$ and circular sector, you get: $$ \sin(x)<x<\tan(x) $$ from what you have: $$ \cos(x)<\frac {\sin(x)}{x}<1 $$ from which immidiately follows that $\lim_{x\rightarrow 0}\frac {\sin(x)}{x} = 1$

Don't you think that this kind of proof is not honest. I mean, in the proof we use the fact that the area of sector is $\frac12xr^2$. This formula comes from integrating (an "infinite" sum of "infinitesimal" triangles' areas). So, roughly speaking, we somehow implicitly use that the length of "infinitesimal" chord $BC$ is equal to the length of "infinitesimal" arch $rx$, which is equivalent that $\lim_{x\rightarrow 0}\frac {\sin(x)}{x} = 1$.

Do I miss something?

If you want a real (honest) proof, read some Real Analysis book. Calculus is not concerned in proving, but in calculations (with some informal proves sometimes). — Integral, Jan 09 '15 at 14:58
Maybe the area of circle comes from integrating area of rings, and the area of sector is thought to be proportional to the centre angle? — peterwhy, Jan 09 '15 at 15:07
Why would one use this proof when this is simply $cos$ and/or equivalence? I mean it does not seems to me clearer or anything. — servabat, Jan 09 '15 at 15:14
@Arkamis: If one were to understand l'Hopital's rule primarily in terms of speed, as opposed to its geometric interpretation, such a proof might not be as far-fetched as one might think. — Lucian, Jan 09 '15 at 15:48

score 7 · Answer 1 · answered Jan 09 '15 at 16:13

The dishonest part is perhaps only in neglecting the question: What is $x$ anyway?

"Size of angle" is nothing that can really be handled. "Length of the arc" is slightly problematic because one has an immediate definition of length only for line segments. But we can introduce a notion of "length of a curve" by approximation with polylines and the notion of "area of an arbitrary figure" via (approximate) exhaustion with triangles. With what the old Greeks knew esp., without calculus) we can still argue that the area of the sector can be exhausted better and better to arbitrary precision, while at the same time approximating the arc by by better and better polylines, and that the quotient of area approximation by arc length approximation gets arbitrarily close to the radius (because those tiny triangles heights approach the radius). In this sense we get the claimed inequality between the areas.

score 6 · Accepted Answer · answered Jan 10 '15 at 04:47

It is a perfectly honest proof, but it is based on few assumptions about areas bounded by plane curves and the definitions of trigonometric functions. The main assumption is that a sector of a circle has an area. The proof of this assumption requires real analysis/calculus but it does not require the limit $\lim_{x\to 0}\dfrac{\sin x}{x}=1$. Once this assumption is established, the next step is to define the number $\pi$ as area of unit circle (circle of radius $1$).

Next we consider the same figure given in question. We need to define a suitable measurement of angles. This can be done in many ways, and one of the ways is to define the measure of $\angle CAB$ as twice the area of sector $CAB$. Note that for this definition to work it is essential that radius of sector is $1$ (which is the case here).

Further we define the functions $\sin x,\cos x$ in the following manner. Let $A$ be origin of the coordinate axes and $AB$ represent positive $x$-axis. Also let the measure of $\angle CAB$ be $x$ (so that area of sector $CAB$ is $x/2$). Then we define the coordinates of point $C$ as $(\cos x,\sin x)$.

Now that we know these assumptions, the proof presented in the question is valid and honest. This is one of the easiest routes to a proper theory of trigonometric functions. The real challenge however is to show that a sector of a circle has an area.

score 4 · Answer 3 · answered Jan 09 '15 at 16:12

The area $\pi r^2 x$ does not require calculus. Something equivalent to this is probably in Euclid.

Where that argument is "dishonest" (or more charitably, anachronistic) is in textbooks that only much later rigorously define the trig functions, using integrals or derivatives.

score 0 · Answer 4 · answered Jan 10 '15 at 05:13

Note from the geometric observation you gave, $\cos(x)<\frac{\sin(x)}{x}<1$ is true for all values of $x$ in between $0$ and $\pi/2$, with this triple inequality also holding for values of $x$ in between $-\pi/2$ and $0$ (why?), so it does not just hold for "infinitesimals," if that is what your concern here is. Taking left-hand and right-handed limits to zero, then, yields $\lim_{x\to0}\cos(x)=1$ and $\lim_{x\to0}1=1$ for both ends of the inequality, as both of these functions are continuous at $x=0$.

Thus, $\lim_{x\to0}\frac{\sin(x)}{x}$ exists and equals 1 by the Sandwich Theorem. Varberg's Calculus is an example of an elementary calculus text which utilizes this useful theorem to the early solution of this problem.

Is the usual proof of $\lim_{x\rightarrow 0}\frac {\sin(x)}{x} = 1$ an honest proof?

4 Answers4

Linked

Related