What is a function?

Question

I have been quite confused by the definition of functions and their uses.. First of all can one define functions in a clear understandable way, with a clear explanation of their uses, how they work and what they do?

Also I have some specific questions regarding functions
Let me give you a examples:

1. $y = f(x) \rightarrow$ This is one of the main reasons I have difficulties understanding functions...
   What does the above statement tell me, and if $y$ is a function why do we use $y=$ at all for a formula like $y = mx + b$ would it be the same as writing $f(x) = mx + b$?
2. Something like $y = x^2$ is apparently a function...... but where is the function name? Which is the input and which is the output?
3. Lastly another example : Let me suppose $f =$ distance
   $f(t) = t^2$
   $f(2) = 4 \rightarrow$ Does this mean distance is $4$.. which is the input which is the output?

Mainly what I'm looking for in an answer is a clear and 'easy' explanation with examples to help me understand this new topic

Answer 1

I see there are already a few answers to this question but I'm going to try my hand at answering it the way I see it.

A function $f$ is a mathematical object that relates elements of two sets, one called the domain $A$ and one called the codomain $B$. The notation $f : A \to B$ denotes the fact that $f$ is a function with domain $A$ and codomain $B$.

What it means to be a function $f : A \to B$ is this: $f$ assigns to each element of $A$ exactly one element of $B$. If $a \in A$, the notation $f(a)$ denotes the element of $B$ to which $a$ is assigned by $f$.

Those elements of $B$ which can be written in the form $f(a)$, for some $a \in A$, are called values of $f$. The set of all values of $f$ is the image of $f$, which is a subset of $B$ (and not necessarily all of $B$).

---

There are various ways of specifying functions. For example:

• If $A$ is finite, you can simply list the values of $f$. For example we can define a function $f : \{ 1,2,3 \} \to \{ \text{red}, \text{green}, \text{blue} \}$ by $$f(1) = \text{green}, \quad f(2) = \text{blue}, \quad f(3) = \text{red}$$
• Sometimes functions can be defined by an equation. An example of a function $f : \mathbb{R} \to \mathbb{R}$ is the one defined by the equation $$f(x) = x^2+3$$ This equation is not itself a function. What it means is, given an element $x \in \mathbb{R}$, the value of $\mathbb{R}$ associated by $f$ with $x$ is $x^2+3$. The expressions $f(x)$ and $x^2+3$ both denote exactly the same thing here: the real number associated with the number $x$. For example $f(2)$ denotes the same thing as $2^2+3$, which in turn denotes the same thing as $7$. The function is $f$, and $f(x)$ denotes the value of $f$ at a given number $x$.

---

The graph of a function $f : A \to B$ is the set $$\{ (a,b) \in A \times B : b = f(a) \}$$ Sometimes, particularly when $f : \mathbb{R} \to \mathbb{R}$, it is convenient to define a function in terms of its graph. (Indeed, $\mathbb{R} \times \mathbb{R}$ what you're depicting when you draw a pair of coordinate axes.) For example the equation $y=x^2+3$ specifies a function $f : \mathbb{R} \to \mathbb{R}$ whose graph is the set $$\{ (x,y) \in \mathbb{R} \times \mathbb{R} : y=x^2+3 \}$$ That is, the function $f$ specified by this equation is the one which associates to each $x \in \mathbb{R}$ the value $x^2+3$. Some people would then say '$y$ is a function of $x$', but this is slightly misleading: what it means is that there is a function whose values are exactly the values of $y$ satisfying the given equation.

---

An example of how a function works is as follows. Suppose a bird is flying in a straight line at a constant speed of $12$ metres per second. The distance the bird flies 'is a function of time', in the following sense: if $t$ is a positive real number, then the distance flown by the bird in $t$ seconds is $12t$ metres. Thus the relationship between distance and time defines a function $d : \mathbb{R}^+ \to \mathbb{R}$, which is defined by the equation $$d(t) = 12t$$ for all $t \in \mathbb{R}^+$. Thus you can consider $d$ as being the 'distance function', and for each $t$ you can consider $d(t)$ as the 'distance travelled at time $t$'.

---

Some non-examples of functions are:

• $f : \mathbb{R} \to \mathbb{Q}$ defined by $f(x) = x$. This is not a function because, for example, $f(\sqrt{2})=\sqrt{2}$, which is not an element of $\mathbb{Q}$.
• $f : \mathbb{R}^+ \to \mathbb{R}$ defined by $f(x)^2=x$. This is not a function because, for example, the expression $f(1)$ has more than one possible value satisfying the equation, namely $1$ or $-1$.
• $f : \mathbb{R} \to \mathbb{R}$ defined by the graph $x^2+y^2=1$. This is not a function because the values of $y$ are not uniquely determined by the values of $x$, for example $0^2+1^2=1$ and $0^2+(-1)^2=1$.

---

In summary, if $f : A \to B$ is a function, then

• $f$ is the function itself, which has domain $A$ and codomain $B$;
• $f(a)=(\text{expression in terms of}\ a)$ is an equation which specifying $f$ by declaring its effect on the elements of $A$; the expression $f(a)$ is not itself a function ($f$ is the function), but a function is determined by its values, so specifying $f(a)$ suffices;
• $y=f(x)$ is an equation that specifies $f$ in terms of its graph.

---

In the mathematical branch of set theory, which is used as a foundation for most mainstream mathematics, we need to specify precisely in terms of sets what it means for $f$ to be a function. In this setting, a function $f : A \to B$ is usually defined to be its graph: that is, if $f$ assigns to each $a \in A$ the value $f(a) \in B$, then we'd write $$f = \{ (a,b) \in A \times B : b=f(a) \} \subseteq A \times B$$ This formal approach isn't something you need to worry about if you're learning about functions for the first time. All that matters is that for every element of the domain $A$, $f$ identifies that element with exactly one element of the codomain $B$.

---

This explanation is woefully incomplete, but there's only so much you can do in an MSE answer... let me know if you need more clarifications.

Answer 2

A function requires some inputs and for each valid combination of inputs produces one output. What is valid is determined by the domain, which is sometimes specified but sometimes left for the reader to infer. The issue is when talking about graphs, because historically people have used single letters to refer to changing quantities, and still do so in many areas of mathematics. When we say that "$y$ is a function of $x$" it means that "$y$ changes together with $x$". That concept does not correspond directly to the proper definition of functions.

As you realize, when you have a straight line it can be described by the linear function $f$ where $f(x) = mx+c$ for any $x \in \mathbb{R}$, with $m,c$ as some fixed values. Notice that everything here is fixed. $f$ is a fixed unchanging object called a function. "$f(x)$" is a notation to denote the output when $x$ is given as input to $f$.

To use your other example, if $f$ is a function such that $f(t) = t^2$ for any $t \in \mathbb{R}$, then $f(0) = 0^2 = 0$, and $f(2) = 2^2 = 4$, and so on. This shows that if you give a different input to a function, you may get a different output. But the function itself hasn't changed. It always does the same thing. If you give it the same input many times in a row, it is going to give you the same output each time. Neither is the input changing. You can give it different inputs, but you cannot give an input that 'changes'.

Note also that the variable used as the input in defining a function is not important and is called a dummy variable. In the above example we could have defined $f$ to be such that $f(u) = u^2$, and it would make no difference.

So "$y = f(x)$" and "$y = x^2$" are actually misleading notations because it is used to denote $y$ changing when $x$ is changed. I wouldn't use it as far as possible. If you really need to write something like "$y = x^2$", you should understand it as follows: When $x = 3$, $y = 9$. When $x = -2$, $y = 4$. Note that such notation is often used in the context of plotting graphs, but then remember that these are just equations describing what points are in the graph, and equations are not the same as functions.

Moreover, some graphs (and their associated equations) do not even correspond to a function, such as "$x^2+y^2 = 1$". What we can say is that this equation describes the set of points in the Cartesian plane that make up the unit circle, but it does not correspond to a function that produces $y$ given $x$, because for instance there are two solutions when $x = 0$, namely $y = 1$ or $y = -1$. A function cannot produce two outputs.

For a concrete example, if say you are told that the position of a ball above the earth's surface is $at-\frac{1}{2}gt^2$ at time $t$, that can be represented by the function $f$ such that $f(t) = at-\frac{1}{2}gt^2$, and we can say that the position of the ball is $f(t)$ at time $t$. We can also plot the ball's trajectory over time by plotting the points $(t,f(t))$ for various values of $t$. It is not correct to say that $f$ is the position at time $t$, because $f$ is just a function and not a value, and remember that "$t$" in the definition of $f$ is a dummy variable and hence meaningless outside the definition. Instead, you either say that $f(t)$ is the position at time $t$ or you say that $f$ is the function that maps any given time to the position of the ball at that time.

For an example of a function with multiple inputs, consider a function $d$ such that $d(x,y) = \sqrt{x^2+y^2}$ for any $x,y \in \mathbb{R}$. $d(x,y)$ is in fact the Euclidean distance of a point $(x,y)$ from the origin. Note that it is valid to take the square-root since $x^2+y^2 \ge 0$ for any $x,y \in \mathbb{R}$. In general whenever we define a function we should think about whether the definition is valid, which means that it must give a well-defined output for any valid combination of inputs.

For another example, consider $\max$ such that $\max(x,y) = \cases{ x & if $x \ge y$ \\ y & if $x < y$ }$. The notation used here is a way of defining different values in different cases. In this example $\max(x,y) = x$ if $x \ge y$ and $\max(x,y) = y$ if $x < y$. Note that the order of the inputs matters.

In general a lot of things in mathematics can be thought of as functions. $x+y$ can be thought of as $\text{sum}(x,y)$ where $\text{sum}$ is a 2-input function. $x<y$ can be thought of as $\text{lessthan}(x,y)$ where $\text{lessthan}$ is a 2-input function that outputs a boolean ($true$ or $false$). When a function's output is always boolean, the function can be called a predicate, which plays a major role in logic.

Finally, I did not talk about set theory because that is not the only way of defining a function and is in my opinion not the most intuitive way. What I said above holds whether functions are defined in terms of sets or not.

Answer 3

I'm going to take a little bit of a different approach from that commonly found in textbooks, and instead of giving you mathematical explanations and examples, I'll try to explain it in terms of the semantics and usage of functions. It seems to me that this where the confusion actually lies (not just for you - for most other people too.)

First off, the definitions others have posted here and that you probably can find in your textbook are correct. I'll put it into layman's terms:

A function is a relationship between a set of inputs and outputs, where each input produces only one output.

That's a pretty broad definition, which probably doesn't sound too useful, and which also probably doesn't go far in explaining all of the $y = x$ and $f(x) = x^2$ stuff you are seeing.

So let's think about this definition a little bit first. What we are talking about is an abstract idea - we are talking about the concept of a "thing" which takes in information and gives back some other information. What makes a function special is the requirement that it has to be predictable - one input can't give two or more different outputs.

This isn't too hard of an idea to grasp - you are already familiar with lots of things that do that. For example, 2 + 2 = ? You know the answer to this is four - you look at the + symbol, then look at the inputs: 2 and 2, and you know you are supposed to add them together. Here the + symbol is an operator that represents the addition function. This is a language used to represent the abstract concept of addition, and we use it so that we can communicate the idea of adding two numbers together to get a sum in a concise manner.

I think this is where you are getting stuck. You know that if you have something like:

$$ y = mx + b $$

that you can "plug in numbers" for m, x, and b, then follow the order of operations to get an answer for y = ?

You also said that we can just write $f(x) = mx + b$, which is true. Why don't we? The answer is: it's just semantics. The concept of taking some numbers, plugging them into an expression, and evaluating to get a single answer is the function. $y = mx + b$ is a representation of the function - it's a convenient, concise notation. The same is true for $f(x) = mx + b$.

So why do we have both notations, and what is their use? Well, the one you are used to: $y = mx + b$ is good when y represents some quantity, measurement, or other thing that you understand pretty well. For example, this is a linear equation, and since we typically plot lines on Cartesian axes and label them x and y, in this case y would represent the y-coordinate of points on the line. We usually graph independent variables on the x axis, so $x$ is typically our input. $m$ is the slope and $b$ is the y-intercept, and these don't change for a given linear relationship, so we call them parameters - they define the linear function. Since we are used to seeing it written like this in this context, there is not much confusion about what the inputs and outputs are - $x$ is usually the input, $y$ is usually the output. The notation matches up with the common usage, and it's convenient and simple, so we use it.

The new notation - the one that is confusing, with the $f(x)$ [and later the $g(x)$ and $h(x)$ and really anything(anything_else)] serves a slightly different purpose. The $f(x)$ part tells you what the inputs are, explicitly. If I say $f(x) = mx + b$, I am telling you directly that x is an input. Once I "plug in" a value for $x$, then whatever the right hand side ends up evaluating to is the output.

So why would we want to use this? For a linear equation, we probably wouldn't, at least not in most cases. When learning this stuff though, we often start with that so that you can see how it all works. There are two major advantages to $f(x)$ notation, though:

1. You can exactly communicate what the intended input variables are
2. You can write an expression for a function even when you don't know what the exact relationship is

#2 is very important. This is why you need to learn this notation at this level - because soon you are going to start working with functions in an even more abstract sense - you will do things like this:

"I have this big equation with $y$ in it that I can't solve yet. I know that y is a function of x and t, but I don't yet know what that relationship is. So, I'll let $y = f(x,t)$, then use that as a placeholder while I do a bunch of things like take derivatives and integrate in order to solve the main problem."

In other words, it lets us write down what we do know when we don't know everything, which happens pretty often.

Now you probably have the answers to your three questions from reading that, but just in case it wasn't clear:

y=f(x)→ This is one of the main reasons I have difficulties understanding functions... What does the above statement tell me, and if y is a function why do we use y= at all for a formula like y=mx+b would it be the same as writing f(x)=mx+b?

It would be the same - we use $y$ when we don't need to be very clear about which variable(s) are inputs.

Something like y=x2 is apparently a function...... but where is the function name? Which is the input and which is the output?

This function has no name yet - although you could just say "the function y equals x squared." More likely you would say "y is a function of x." The function happens to be $f(x) = x^2$

Lastly another example : Let me suppose f= distance f(t)=t2 f(2)=4→ Does this mean distance is 4.. which is the input which is the output?

Yes, if distance $d$ is a function of t, and $d = f(t) = t^2$, then when $t = 2$, $d = 4$. The input is 2, which is "plugged in" to the variable $t$, and the output is 4 - the answer you get after evaluating the expression.

Answer 4

I think it is important to note that there are two different, but closely related concepts called “function”. To avoid confusion, I will use the term “map” for one of them and “dependent variable” (for the lack of a better word) for the other.

A map is what is described in Clive’s answer. It is something, a blackbox if you will, that takes values from some set as inputs and returns values from a – potentially different – set as outputs. The important thing is that there exists an output for every input element and that there is only one. Furthermore, the output must be the same whenever the input is the same.

Sometimes, you don’t know anything about the map, but at other times, the map is explicitly given, as in for example $$f : \mathbb{R} \to \mathbb{R}, \\ x \mapsto x^2 + 1,$$ or, which is the same, $$f : \mathbb{R} \to \mathbb{R}, \\ f(x) = x^2 + 1.$$ In this case, the name of the variable $x$ is irrelevant in principle. It is just needed so we can talk about the input element. The same function would be defined by say $$f : \mathbb{R} \to \mathbb{R}, \\ t \mapsto t^2 + 1.$$ (But in practice it isn’t, see below.)

Finding the output for a given input is easy in this case: Just replace every occurrence of the variable to the left of $\mapsto$ by the input (adding parentheses as necessary). In our example: $$f(5+3) = (5+3)^2 + 1 = 64 + 1 = 65.$$

In general, we write $f(x)$ for the output value of the function $f$ for the input value $x$. In short, the value of $f$ at $x$ or $f$ of $x$.

This concept is useful because it allows us to not only talk about values but about functions themselves. They are objects an can thus be given as inputs or outputs to other functions, for example. Also, it is easier to define and manipulate formally, in my opinion.

Closely related is what I will call a dependent variable. This is a variable whose value depends upon the value of another variable and it changes as the other variable changes (note that we didn’t need the concept of “changing variables” above).

For example, $$y = x^2 + 1.$$ In this case, the name of the variable $x$ does matter. $$y = t^2 + 1$$ would be something different. In the first case, $y$ changes as $x$ changes, in the second case, $y$ changes as $t$ changes.

If you want to know the value of $y$ when $x = 5 + 3$, replace $x$ by $5 + 3$ in the right hand side of the first definition. It is not really sensible to ask for the value of the second $y$ when $x = 5 + 3$ unless there are further relations between $x$ and $t$ not given here.

To denote the value of $y$ as $x$ takes some value, one sometimes uses $y(x)$, for example $y(5+3)$, leaving implicit that $x$ is to substituted. I will use $y|_{x=5+3}$ instead.

The first advantage of this concept are that it is shorter. Note that we didn’t need to repeat the name of the variable we used to define $y$ as we did with $f$. In addition to that, functions in applications oftentimes have multiple inputs. Having fixed helps to remember their purpose. This is one of the reasons physicists usually prefer this concept. Also, I think this concept is older (but don’t quote me on that).

I claimed that these concepts are closely related and here is why:

If $y$ is a variable depending upon $x$, then there exists some function $f$ such that $$y = f(x).$$ And whenever $f$ is a function, we can define $$y = f(x)$$ and then $y$ is a dependent variable (depending upon $x$). This is why $y$ is called a function of $x$.

As both concepts are useful, in practice one likes to mix them and call both of them function, which I don’t find useful. We have already seen the mixed notation $y(x)$. Similar things are true for example with derivatives, where $\frac{\operatorname{d} f}{\operatorname{d} x}$ doesn’t really make sense (because the function would be same if we used the variable $t$ in its definition) and $y’$ doesn’t really make sense (because it isn’t clear which dependency of $y$ is meant). Still, both of these notations are common in addition to the sensible versions $f’$ and $\frac{\operatorname{d} y}{\operatorname{d} x}$.

You will have to learn to switch between the two concepts.

Answer 5

Roughly speaking, a function is a rule that produces an output value from a given input value. You can think of it as a machine, if you like: you feed it an input, it performs some process on this input, and produces an output.

In principle, the inputs and outputs can be anything. But, to make things clearer, let's just focus on the case where the inputs and outputs are numbers, for now.

An example of a rule that defines a function is: take the input, square it, and then divide by two. When you input the number $3$ into this function, it gives you back the output $9/2$. When the input is $1$, the output is $1/2$, and so on. In symbols, if the input is $x$, the output is $x^2/2$. So, we might write this function as $x \mapsto x^2/2$, in which case we would refer to it as "the function that maps $x$ to $x^2/2$". Sometimes this gets abbreviated, and people just say "the function $x^2/2$". There's nothing magic about the variable name "$x$"; we could write $w \mapsto w^2/2$, instead, and this would still denote the same function -- it's still a machine that squares and then halves its input.

Very often, it's convenient to give a name to a function. The function we described above could be called the "square-and-halve" function, but something shorter would be nice. We might choose to give our square-and-halve function the name "$f$". The rule defining this function could then be written as $f(x) = x^2/2$. This is just a shorthand way of saying "given the input $x$, the function $f$ produces $x^2/2$ as output". Again, we don't have to use the symbol "$x$" to denote the input; writing $f(t)=t^2/2$ would still define the same square-and-halve function.

As we noted earlier, the square-and-halve function produces the output $9/2$ when its input is $3$. We denote this by writing $f(3) = 9/2$. You could read this as "the function $f$, when applied to the input $3$, gives the output $9/2$".

Answer 6

The term function hasn't always meant what it does now. Originally it was a formula that expressed one variable in terms of another. It wasn't even necessary that the value of the other variable be uniquely determined by the one variable.

In the 17th century, Newton, in his Principia Mathematica implicitly assumed that all functions were differentiable, and that was more or less correct in his time under that meaning of function at the time.

In the 18th century Euler and others found other expressions for functions, in particular, trigonometric series (i.e., Fourier series). These didn't always define continuous or differentiable functions. Consequently, the concept of function expanded.

In the 19th century the concept changed in a couple of ways. Functions had to have a unique value, that is, the value of the dependent variable had to be uniquely determined by the value of the independent variable. Those functions that didn't have that property were named multivalued functions, a term still in use. Also, functions had become common that didn't have real values and real arguments, but some other kinds of values and arguments.

By the 20th century, set theory had been developed, and a function $f$ could be identified with its graph $y=f(x)$, a certain subset of the product set $D\times E$ where $D$ was the domain of $f$ and $E$ the codomain of $f$. (The terms range and image were sometimes used for codomain but they often mean something else now.)

Thus, one current definition of a function $f$ from one set $D$ to another set $E$, written  $f:D\to E$, is a subset  $f\subseteq D\times E$ such that for all $x\in D$, there exists a unique $y\in E$ so that $(x,y)\in f$. That last condition, $(x,y)\in f$, is usually written $y=f(x)$.

Even now, although we have a different concept of functions, they are still often defined as they always were, by formulas.

Answer 7

Summary

A function is something that takes in a number, changes it according to some rule, and spits out another number. That's it. That's all. The rest is notation.

Simpler Definition

When I was in 4th and 5th grade, when we talked about functions, we talked about them in the context of function "machines" - those cute little things that took in a number and spit another one out, something like these tables:

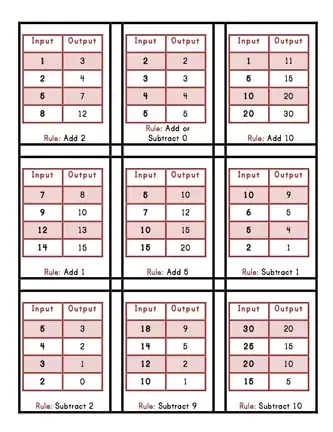
Later, the rules would get harder. And the rules were what were called "functions". So this is what a function is, at its most fundamental level: something that takes in a number, and spits out another number according to a predetermined rule.

Middling Definition

Then, in 6th or 7th grade, we started talking about functions as equations. These rules from the function machines could be written as equations, that took in an input $x$ and spit out an output $y$. These functions could be graphed on the Cartesian plane, like so:

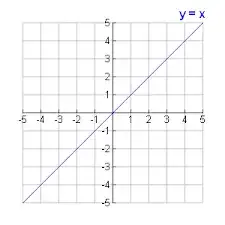
We learned that the points on this line were representative of inputs and outputs - the x-coordinate represented the input, and the y-coordinate represented the output. The equations, of course, could be more complex, and you could also write them as $f(x) = x$ (instead of $y=x$) and we were told this was function notation, and it would be useful later.

Set Theory Definition

More recently, outside of school, I learned the more formal definition of a function, using set theory. First, a few quick pieces of terminology/notation, and we'll be on our way.

The "naive" definition of a set is that a set is a collection of any number of objects, normally numbers but sometimes other things. This actually turns out to be not quite right, and if you follow it along far enough, it leads to a paradox called Russell's Paradox, but for our purposes, we can stick with this definition. So we might have a set like $A = \{4,5\}$ and a set $B = \{4,5,6\}$.

First, we can define an element of a set - that is, a number or object that is within that particular set. For example, here we can say $4 \in A$, or that $4$ is in $A$. We can also define a subset of a set. To be a subset of another set, the supposed subset's elements must all be in the other set. For example, $A$ is a subset of $B$ (written $A \subset B$) because $4$ and $5$ are both in $B$.

Next, we can define multiplication of sets. To do this, I'd like to use two different sets for the example, so we'll define the sets $A = \{a,b\}$ and $B = \{c,d\}$. The answer here is not quite what you might expect - it is $A \times B = \{(a,c),(a,d),(b,c),(b,d)\}$. In other words, it is the set of ordered pairs that can be created from the two sets such that the ordered pair is of the form $(x, y)$ where $x \in X$ and $y \in Y$.

Another important thing to keep in mind here is the set of all real numbers, $\mathbb{R}$. If we do $\mathbb{R} \times \mathbb{R}$ (which can be rewritten as $\mathbb{R}^2$) we get the set of all real coordinates in the second dimension. This makes sense, especially if you think about $\mathbb{R}$ as being the set of all real coordinates in the first dimension. You can further think about this as $\mathbb{R}^n$ being the set of all real coordinates in the $n$th dimension. Cool, huh?

Carrying on, let us define a relation, another key piece of the puzzle. A relation $R$ between two sets, $X$ and $Y$ is a subset $R \subset Y \times X$. To say that $x \in X$ is related to $y \in Y$ we can write $yRx$. So, what exactly does this mean? Well, let's consider the relation $=$ on $\mathbb{R}$. It is the line $y=x$! Does this make sense? We are dealing with the set of all real numbers and have effectively set up a connection between some value $x$ in the set of all real numbers and some value $y$ in the set of all real numbers. We've created what is almost a function!

So, now we get to functions. A function $f$ between $X$ and $Y$ is written $f: X\rightarrow Y$. It is a relation on $Y \times X$ such that $yfx$ and $y'fx$ implies $y=y'$ - in other words, a function is a relation that "maps" or connects every $x$ to a unique $y$.

Uses

Oh, man. There are so many uses for these things I don't know where to start! They're used for anything that involves taking in a number, changing it according to a rule, and spitting out a new one, obviously. Many disciplines do this sort of thing, like physics, economics, engineering, computer programming, finance, and I could keep going. Functions could be thought of as one of the most widely used mathematical tools.

Finally, something to consider here, is behind all of these mathematical definitions and all of this notation is a fundamental idea: quantities in our world are related, and we can show how they are related using simple rules! Think about a circle. The radius of the circle is related to the area of the circle by a simple equation - $A = \pi r^2$. That's a function! It takes in a number, $r$, and spits out a number, $A$.

Example

I'm going to define a distance function here, a metric. Imagine a set $X$ with a function $d: X\times X \rightarrow \mathbb{R}$ such that

1. $d(x,y) = d(y, x)$ for all $x,y \in X$ - in other words, the distance between two numbers is the same whether they are listed one way or another.
2. $d(x, y) \geq 0$ with $d(x,y)$ only equal to zero if $x=y$ - basically, distance can't be negative, and the distance can only be zero if it is the same point.
3. $d(x,y) \leq d(x,z) + d(z,y)$ for all $x, y, z \in X$ - this is known as the Triangle Inequality, and a quick illustration should make it pretty clear.

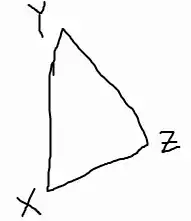
Sorry, pretty lopsided triangle, but oh well. The distance between $x$ and $y$ cannot be greater than the distance between $y$ and $z$ plus the distance between $y$ and $x$, which really makes a whole lot of sense. You can only increase the distance by adding another point.

So we just defined a distance function! Not so bad, really.

Specific Questions

Okay, last bit, to answer your specific questions.

1. $y=f(x)\rightarrow$ This is one of the main reasons I have difficulties understanding functions...What does the above statement tell me, and if $y$ is a function why do we use $y=$ at all for a formula like $y=mx+by$ would it be the same as writing $f(x)=mx+b$?
2. Something like $y=x^2$ is apparently a function...... but where is the function name? Which is the input and which is the output?
3. Lastly another example : Let me suppose $f=$ distance $f(t)=t^2$ $f(2)=4\rightarrow$ Does this mean distance is 44.. which is the input which is the output?

1. I will be updating with the answer to this one.
2. Yes, it is a function - $y$ is the output and $x$ is the input. You can rewrite it as $f(x) =x^2$ if you wanted. This is just another way to write the basic concept.
3. I will be updating with the answer to this one.

Finally...

There are several things that can be done with functions, like composition, and all sorts of other stuff that would take a bit to go into here (hmm...maybe I'll add some of that at a later date). For now, I'd recommend looking at the wikipedia page on functions, and sites like Khan Academy, and of course asking questions when you have them.

Hope this helps!

Answer 8

1) Loosely speaking, a (numerical) function is any rule that associates, to any number in a certain set, another number. If the function is given the name $f$, and if $x$ is in the set (which is called the domain of the function), the corresponding number is denoted f(x). The function $f$ is different from the particular number $f(x)$.

You can see it as a key on a pocket calculator: the sin key would be the sine function; when you enter the number 30 as $x$, then press the ‘sin’ key, you get 0.5, which is the value of the sine function at 30 degrees – at least if your calculator uses angles in degrees for trigonometric functions. Usually you write this as $sin(30)=0.5$.

2) $y=x^2$ is a way to define the square function, but it is given no name. Strictly speaking, one should write: ‘Let $f$ be the function defined by $f(x)=x^2$’ rather than the shorthand: ‘Consider the function $y=x^2$’. The input is $x$ and the output is $x^2$.

3) In $f(2)=4$ (in this particular, I would rather name the function ‘$d$’ – you can give a function any name you please), the input is 2 and the output is 4.

Answer 9

A function is a set of mathematical operations performed on one or more inputs (variables) that results in an output. For now, functions will take one or more real numbers as an input, and return a numerical output. In more advanced classes you'll learn about far more complex functions! However, a simple function might return the input plus one. Such a function would look like:

Y = X + 1

In this case, X in the input value, and Y is the output. By putting any number in for X, we calculate a corresponding output Y by simply adding one. The set of possible input values is known as the domain, while the set of possible outputs is known as the range.

Here are two more examples of what functions look like:

1) y = 3x - 2

2) h = 5x + 4y

Let's examine the first example:

In the function, y = 3x - 2, the variable y represents the function of whatever inputs appear on the other side of the equation. In other words, y is a function of the variable x in y = 3x - 2. Because of that, we sometimes see the function written in this form:

f(x) = 3x - 2

What does f(x) mean?

That means just the same as y= in front of an equation. Since there's really no significance to y, and it's just an arbitrary letter that represents the output of the function, sometimes it will be written as f(x) to indicate the the expression is a function of x. Note that you'll also see it written as g(x), h(x), and so forth, but f(x) is the most common because function starts with the letter f.

Answer 10

You're at a table. There are some objects laid out in front of you. You have a sheet of labels. You apply all of the labels. An object can have zero or more labels, but every label must be on exactly one object.

The domain is the labels. The codomain is the objects (including those that don't get labeled). The function is your choice of labeling. The function space is all possible choices of labeling. A function could even be manifest as a picture of the table with its labeled objects, and then you could treat this picture as a label or as an object for another function.

If your choice of labeling follows a simple rule, then there's a simple way to describe your choice of labeling. For example, imagine the labels are a copy of the real numbers, and the objects are another copy of the real numbers.

Maybe your rule is that an object is twice as big as the label attached to it. Then your choice of labeling could be described as "$x \mapsto 2x$".

Or maybe your rule is that the "$0$" label goes on the "$1$" object, and furthermore, that if you place each labeled object in the Cartesian plane, where the label corresponds to its left-right position and the object itself corresponds to the down-up position, then the slope of the curve at any point equals the object itself. Then your choice of labeling could be described as "$\exp$", or equivalently as "$x \mapsto e^x$".

In either case, $x$ is not a variable. It's merely a placeholder in the description. It has no other meaning. You could use any symbol as a placeholder; the choice of "$x$" is arbitrary.

Although not every function has a simple rule to describe it, you can still name any function you can think of. You could even say "let $f:\mathbb{R}\rightarrow\mathbb{R}$" (i.e. "assume $f$ is some choice of how to label the real numbers with the real numbers") and then proceed to draw conclusions armed only with the knowledge that $f$ is an object in the space of real-valued functions.

If a function's name is "$f$", then we pronounce "$f(1)$" as "$f$ of $1$", and what we really mean is "the object that $f$ assigns the label $1$ to." Even if all you know about $f$ is that $f:\mathbb{R} \rightarrow A$, you still know $f(1)$ is an object from the set called "$A$".

---

To the OP's specific examples:

"$y=f(x)$" is an equation. Every equation is merely a statement of fact. It adds some knowledge to the context. It says: "Whatever else we might know (or not know) about $y$, $f$, and $x$, we now know that $x$ is a label in the domain of $f$, $y$ is an object in the codomain of $f$, and $f$ assigns the label $x$ to the object $y$."

"$y=x^2$" is likewise an equation, a piece of knowledge being added to the context. The function is $\square^2$. It's just written differently from other functions.

"$f$ is distance; $f(t)=t^2$; $f(2)=4$" (you could also write "$f = \square^2$") -- this is a claim about the physical system being modeled. A claim that could be true or false, depending on what you observe. The claim is that if you measure time and distance, then the relationship between those measurements is the same as the relationship between labels and objects of $f$.