The coordinate transformation employed in this answer has a couple of references in:
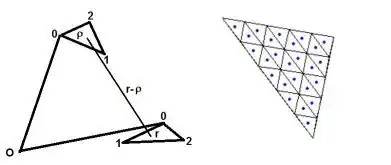
Suppose that the two triangles, with vertices numbered as $(0,1,2)$, are successively described by:
$$\begin{array}{lll}
(r) & : &\vec{r}(\xi,\eta) = \vec{r_0}+\xi\,(\vec{r_1}-\vec{r_0})+\eta\,(\vec{r_2}-\vec{r_0})\\
(\rho) & : &\vec{\rho}(\alpha,\beta) = \vec{\rho_0}+\alpha\,(\vec{\rho_1}-\vec{\rho_0})+\beta\,(\vec{\rho_2}-\vec{\rho_0})
\end{array}$$
with $\,0 \le \xi \le 1$ , $0 \le \eta \le 1-\xi\,$ and
$\,0 \le \alpha \le 1$ , $0 \le \beta \le 1-\alpha$ .
Then the force upon an infinitesimal part $(d\alpha\,d\beta)$ of triangle $(\rho)$
being attracted by an infinitesimal part $(d\xi\,d\eta)$ of triangle $(r)$ is:
$$
d\vec{F} = G\cdot m_r\cdot m_\rho \frac{\vec{r}(\xi,\eta)-\vec{\rho}(\alpha,\beta)}
{\left|\vec{r}(\xi,\eta)-\vec{\rho}(\alpha,\beta)\right|^{3/2}}
2\,d\xi\,d\eta\cdot 2\,d\alpha\,d\beta
$$
Where the factors $2$ comes from the fact that the parent triangles have area $1/2$ instead of $1$ :
$$
2\int_{\xi=0}^{\xi=1} d\xi \int_{\eta=0}^{\eta=1-\xi} d\eta =
2\int_{\alpha=0}^{\alpha=1} d\alpha \int_{\beta=0}^{\beta=1-\alpha} d\beta = 1
$$
The force as a whole with $\vec{r} = (x,y,z)$ , $\vec{\rho} = (a,b,c)$ is:
$$\left[ \begin{array}{c} F_x\\F_y\\F_z \end{array} \right] =
\left[\begin{array}{c}
\int_{\xi=0}^{\xi=1}\int_{\eta=0}^{\eta=1-\xi}\int_{\alpha=0}^{\alpha=1}\int_{\beta=0}^{\beta=1-\alpha}
\frac{4\,G\cdot m_r\cdot m_\rho\cdot (x-a)\cdot d\xi\,d\eta\cdot d\alpha\,d\beta}
{\left|(x-a)^2+(y-b)^2+(z-c)^2\right|^{3/2}} \\
\int_{\xi=0}^{\xi=1}\int_{\eta=0}^{\eta=1-\xi}\int_{\alpha=0}^{\alpha=1}\int_{\beta=0}^{\beta=1-\alpha}
\frac{4\,G\cdot m_r\cdot m_\rho\cdot (y-b)\cdot d\xi\,d\eta\cdot d\alpha\,d\beta}
{\left|(x-a)^2+(y-b)^2+(z-c)^2\right|^{3/2}} \\
\int_{\xi=0}^{\xi=1}\int_{\eta=0}^{\eta=1-\xi}\int_{\alpha=0}^{\alpha=1}\int_{\beta=0}^{\beta=1-\alpha}
\frac{4\,G\cdot m_r\cdot m_\rho\cdot (z-c)\cdot d\xi\,d\eta\cdot d\alpha\,d\beta}
{\left|(x-a)^2+(y-b)^2+(z-c)^2\right|^{3/2}} \end{array} \right]
$$
Where:
$$
\left\{\begin{array}{l}
x = x_0+\xi\,(x_1-x_0)+\eta\,(x_2-x_0)\\
y = y_0+\xi\,(y_1-y_0)+\eta\,(y_2-y_0)\\
z = z_0+\xi\,(z_1-z_0)+\eta\,(z_2-z_0)\end{array}\right.
\qquad \qquad \left\{\begin{array}{l}
a = a_0+\alpha\,(a_1-a_0)+\beta\,(a_2-a_0)\\
b = b_0+\alpha\,(b_1-b_0)+\beta\,(b_2-b_0)\\
c = c_0+\alpha\,(c_1-c_0)+\beta\,(c_2-c_0)\end{array}\right.
$$
A short excercise with MAPLE learns that even calculating the innermost integrals is a disaster.
And it doesn't finish at all with calculating the innermost double integrals. Therefore a "closed form"
seems to be out of reach anyway, unless someone can devise some clever trick.
It has been suggested that it would be easier to calculate the potential energy of a triangle
$(r)$ with respect to a triangle $(\rho)$ :
$$V =
\int_{\xi=0}^{\xi=1}\int_{\eta=0}^{\eta=1-\xi}\int_{\alpha=0}^{\alpha=1}\int_{\beta=0}^{\beta=1-\alpha}
\frac{4\,G\cdot m_r\cdot m_\rho\cdot d\xi\,d\eta\cdot d\alpha\,d\beta}
{\sqrt{(x-a)^2+(y-b)^2+(z-c)^2}}
$$
But, apart from calculating the integrals, I have no idea how to proceed from there to obtain the force.
Numerically
As suggested in a comment by Mr. G , The easiest thing to do would be to just consider both
of the triangles as point masses located at their centers of mass for the purposes of gravity
(this is an approximation, however) :
$$
\vec{F} = G\cdot m_r\cdot m_\rho \frac{\vec{r}(\xi,\eta)-\vec{\rho}(\alpha,\beta)}
{\left|\vec{r}(\xi,\eta)-\vec{\rho}(\alpha,\beta)\right|^{3/2}}
\qquad \mbox{with} \qquad \xi = \eta = \alpha = \beta = \frac{1}{3}
$$
With a subdivision of both triangles, like in the above picture on the right,
the approximation can be made more accurate. Define $N^2$ midpoints in one triangle and $M^2$ in the other:
$$\begin{array}{l}
\vec{r}(i,j) = \vec{r_0}+\frac{i+(1/3\, \vee\, 2/3)}{N}\,(\vec{r_1}-\vec{r_0})+\frac{j+(1/3\,\vee\, 2/3)}{N}\,(\vec{r_2}-\vec{r_0})\\
\vec{\rho}(k,l) = \vec{\rho_0}+\frac{k+(1/3\,\vee\, 2/3)}{M}\,(\vec{\rho_1}-\vec{\rho_0})+\frac{l+(1/3\,\vee\, 2/3)}{M}\,(\vec{\rho_2}-\vec{\rho_0})
\end{array}$$
For suitable integers $\,0 \le i+j < N(-1) \; ; \; 0 \le k+l < M(-1)$ , namely such that all midpoints are inside the main triangles.
But I don't think that implementing such a subdivision is intended by the OP,
because the gravitational force between the two main triangles is meant as simple case in itself. But anyway, then the net force would become:
$$\vec{F} = \frac{G\cdot m_r\cdot m_\rho}{N^2 M^2} \sum_i \sum_j \sum_k \sum_l
\frac{\vec{r}(i,j)-\vec{\rho}(k,l)}
{\left|\vec{r}(i,j)-\vec{\rho}(k,l)\right|^{3/2}}
$$

$2.$ The force due to one triangle acts at every point of the other triangle, which will lead to torques as well as translations.
$3.$ It is almost certainly easier to use the potential formulation if you want an exact answer.
$4.$ The easiest thing to do would be to just consider both of the triangles as point masses located at their centers of mass for the purposes of gravity (this is an approximation, however.)
– Mr. G Jan 02 '15 at 04:50