If the formula for a Tutte polynomial is:
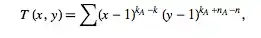
then how does T(1,1) solve for spanning trees instead of just returning a 0?
If the formula for a Tutte polynomial is:
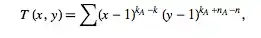
then how does T(1,1) solve for spanning trees instead of just returning a 0?
First, the graph may not be connected, so it should be pointed out that $T(1,1)$ counts the number of maximal spanning forests, not the number of spanning trees.
The answer to your question is that not all summands of $T(1,1)$ are zero. Sometimes a summand will be of the form $0^00^0$, and in combinatorics, we make the convention that $0^0=1$. See here for a discussion about this.
If the graph is connected with $n$ vertices, note that a summand $0^00^0$ occurs precisely when $A\subseteq E(G)$ is such that $|A|=n-1$ and $(V,A)$ has one component (i.e., is connected), and this occurs if and only if $(V,A)$ is a spanning tree.