3

I want to build a paper model of a Goldberg polyhedron, a Icosahedral $G(2,2)$.

But I cant find the formula to calculate the 2 sizes needed for the edges. For a $G(4,1)$ the sizes are here: The model of a large geodesic sphere

Also I need to draw an irregular hexagon with 5 equal-size edges and a 1 larger edge. How can i do that? Or is there a software that can I use?

MarianD
  • 2,953
remi
  • 31
  • One or more of the versions of the Stella app may include the Goldberg polyhedra. If it does, it'll provide a printable net for your model. – Blue Dec 08 '14 at 21:20
  • The Stella app only has a G(1,1) truncated icosahedron, i need a G(2,2) or G(3,1) – remi Dec 09 '14 at 03:53
  • Darn. This answer suggests a program called "polymake", but I've never used it and know if it's really relevant to your problem. I have an algorithm that generates polyhedral coordinates from vertex-adjacency information; it probably won't help here, but it could be worth a shot. Do you have the adjacency matrix of $G(2,2)$ and/or $G(3,1)$ handy? I don't want to have to generate it myself. – Blue Dec 09 '14 at 05:06
  • Have you seen this page of Dual Geodesic Icosahedra? Clicking through each item gives you a list of edge lengths, vertex coordinates, etc. – Blue Dec 09 '14 at 07:26
  • The second link you gave me , http://dmccooey.com/, is great ! but it doesnt show which edge is which. But i did find a 6v geoddesic dome calculator that i can use for a g(2,2) insted of a v6, that also gives me 4 difernt edge lenghts and i get i diagram but the differ form the calculation on your link. – remi Dec 09 '14 at 12:36
  • this is the calculator i mentioned: i just wish the other one would show where the different edges go. Thanks Blue for the help ! – remi Dec 09 '14 at 12:39
  • http://www.domerama.com/calculators/6v-geodesic-dome-calculator/ – remi Dec 09 '14 at 12:41
  • One more potentially-useful software link: Antiprism. It seems that the Dual Geodesic Spheres are generated by built-in commands, such as antiview geo_2_2_d. Again, I haven't used this program. – Blue Dec 09 '14 at 14:00
  • Regarding dmccooey.com: The polyhedral data includes "Faces" (that is, lists of vertices adjacent to the figure's faces). With a little perseverance, you could deduce which edge-lengths go where. It helps that the regular pentagons are easily distinguishable. :) – Blue Dec 09 '14 at 14:06

1 Answers1

2

I'll attempt to answer this specific case, the $G(2, 2)$ Goldberg polyhedron.

For referencing the faces, let's use this photo from Wikipedia:

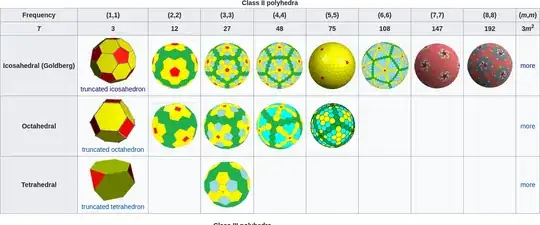
Wikipedia screenshot

We have pentagons, yellow hexagons and green hexagons.

We would like to figure out the following:

  1. Edges between pentagons and yellow hexagons.
  2. Edges between yellow hexagons.
  3. Edges between yellow hexagons and green hexagons.
  4. Edges between green hexagons.

Note that this page already gives the numbers to many decimal places, and clicking on the coordinates button below the picture takes us to this link, which gives the polynomials that need to be solved, if you care about very exact numbers.

Another practical way of calculating the numbers is by creating a geodesic dome in Blender (after enabling the "Add Mesh: Geodesic Domes" addon under Edit » Preferences » Add-ons). Hit Shift+A to add a new geodesic dome. What I find useful is cutting it in half using a boolean modifier and a cube, then find a diagonal of size $R=2$, and taking measurements only on one half of the diagonal, like so:

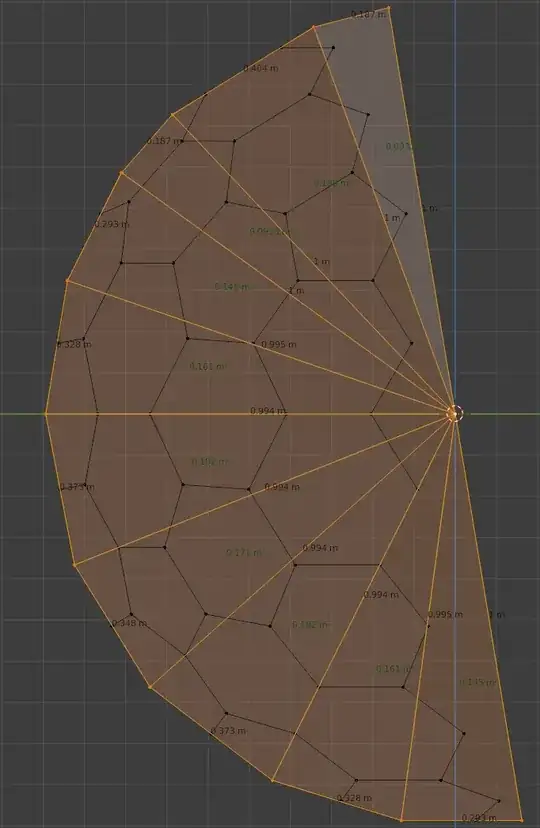
Blender screenshot

I enabled the "Edge Length" and "Face Area" under "Measurement Options", which is available in edit mode (Tab) under "Viewport Overlays" in the top-right corner.

Here we can see the following edges, starting from top, going clockwise:

  1. $0.187m$ — edge between yellow hexagons.
  2. $0.404m$ — diagonal of a green hexagon.
  3. $0.187m$ — edge between yellow hexagons.
  4. $0.293m$ — height of a pentagon.
  5. $0.328m$ — height of a yellow hexagon.
  6. $0.373m$ — height of a green hexagon.
  7. $0.348m$ — height of a green hexagon in another direction.
  8. $0.373m$ — height of a green hexagon.
  9. $0.328m$ — height of a yellow hexagon.
  10. $0.293m$ — height of a pentagon.

Distances between the origin and some vertices (first, second, third, fourth and the last one) are $1$, the distance to the other "vertices" in the cross diagram is less since those are not really edges of the polyhedron. However, those distances can be calculated using the Pythagorean theorem based on the edges they belong to.

Simplifying all these relations should in theory bring you to the 6th order polynomial from the page above.

In any case, Blender is a nice free tool for such concrete measurements, and can help with visualisations as well.

Attila O.
  • 257