Calculation of $ \cos\left(\frac{2\pi}{7}\right)+\cos \left(\frac{4\pi}{7}\right)+\cos \left(\frac{6\pi}{7}\right)$

Question

Calculation of $\displaystyle \cos\left(\frac{2\pi}{7}\right)+\cos \left(\frac{4\pi}{7}\right)+\cos \left(\frac{6\pi}{7}\right)$ and $\displaystyle \cos\left(\frac{2\pi}{7}\right)\times \cos\left(\frac{4\pi}{7}\right) \times \cos\left(\frac{6\pi}{7}\right)$ is

$\bf{My\; Try::}$ Let $\displaystyle \frac{2\pi}{7}=\phi\;,$ Then $3\phi = 2\pi-4\phi\Rightarrow \cos \left(3\phi\right) = \cos \left(2\pi-4\phi\right)=\cos \left(4\phi\right)$

So $4\cos^3 \phi -3\cos \phi = 2\left[2\cos^2 \phi - 1\right]^2-1=2\left[4\cos^4 \phi+1-4\cos^2 \phi\right]-1 = 8\cos^4 \phi-8\cos^2 \phi+1$

So $8\cos^4\phi-4\cos^3 \phi-8\cos^2 \phi+3\cos \phi+1=0$

Now I did not understand how can i solve after that

Help me

Thanks

Answer 1

$\require{color} \definecolor{blue}{RGB}{3,169,244} \definecolor{green}{RGB}{76,175,80} \definecolor{red}{RGB}{244,67,54} \newcommand{\k}[1]{\color{black}{\textsf{#1}}} \newcommand{\b}[1]{\color{blue}{\textsf{#1}}} \newcommand{\g}[1]{\color{green}{\textsf{#1}}} \newcommand{\r}[1]{\color{red}{\textsf{#1}}} \cos\left(\frac{2\pi}{7}\right)+\cos \left(\frac{4\pi}{7}\right)+\cos \left(\frac{6\pi}{7}\right) = -\frac{1}{2}$

Visual proof:

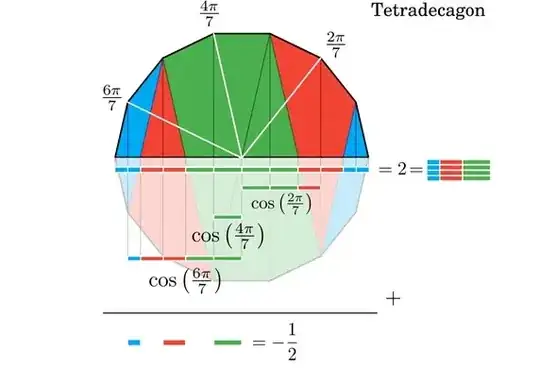
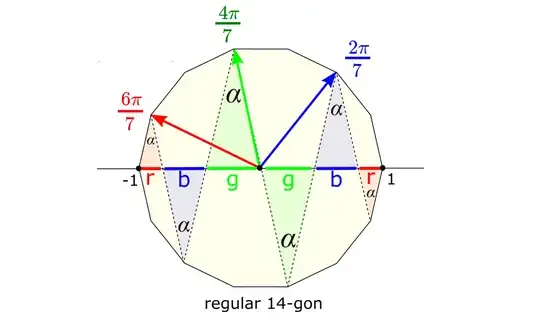
This regular 14-gon has a 'diameter' of 2. This diameter is the sum of four blue segments, four red segments and four green segments. But also each cosine can be expressed as a sum of these segments. Adding the three cosines yields the negative sum of one blue, one red and one green segment, which is $-\frac12$

Further explanation

Inside the regular Tetradecagon, the three cosines are the vertical projections of the nodes at $\{2\pi/ 7,4\pi/7,6\pi/7\}$ onto the horizontal diameter. This diameter ($\textsf{D}=2$) is further divided into twelve smaller segments, by drawing some extra lines from the other nodes at the upper semicircle, located at $\{1\pi/7,3\pi/7,5\pi/7\}$. The angle between all these (near) verticals is always the same, because all chord lengths are similar in a regular polygon. Therefore, the diameter $\textsf{D}$ consists of just three types of segments $\{\b b, \r r, \g g \}$:

$$\qquad \large \textsf{D} = \b{2b} \k + \r{2r} \k + \g{2g} \k{+} \g{2g} \k + \r{2r} \k + \b{2b} \k {= 2}$$

From which follows that:

$$\qquad \large \b{b} \k + \r{r} \k + \g{g} \k{=} \frac12$$

From the image, the sum of the three cosines can be easily expressed in these three types of segments:

$$\qquad \large \begin{align}\cos\left(\frac{2\pi}{7}\right) & = \g{2g} \k{+} \r r \\ \cos\left(\frac{4\pi}{7}\right) & = \k{-}\g g\\ \cos\left(\frac{6\pi}{7}\right) & = -\g{2g} \k{-} \r{2r} \k{-}\b b\\ \hline \\ \sum_{k=1}^3\cos\left(\frac{2k\pi}{7}\right) &= \k{-}\g g \k{-} \r{r} \k{-} \b{b} \k{=} -\frac12 \end{align}$$

$\blacksquare$

Answer 2

\begin{equation} y = \cos\left(\frac{2π}{7}\right)+\cos\left(\frac{4π}{7}\right)+\cos\left(\frac{6π}{7}\right) \end{equation} Dirichlet kernel: \begin{equation} 1+2\sum_{k=1}^{n}{\cos(kx)} = \frac{\sin((n+\frac{1}{2})x)}{\sin(x/2)} \end{equation} For $x=\frac{2\pi}{7},n=3$:

\begin{equation} 1+2y = \frac{\sin((3+\frac{1}{2})\frac{2\pi}{7})}{\sin(\frac{2\pi}{7}/2)}=\frac{\sin(\pi)}{\sin(\frac{2\pi}{7}/2)}=0 \end{equation}

\begin{equation} 1+2y =0 \end{equation}

\begin{equation} y =-\frac{1}{2} \end{equation}

---

\begin{equation} x = \cos\left(\frac{2π}{7}\right)\cos\left(\frac{4π}{7}\right)\cos\left(\frac{6π}{7}\right) \end{equation}

\begin{equation} \cos\left(\frac{6π}{7}\right)=-\cos\left(\frac{π}{7}\right) \end{equation}

\begin{equation} x = -\cos\left(\frac{2π}{7}\right)\cos\left(\frac{4π}{7}\right)\cos\left(\frac{π}{7}\right) \end{equation}

Viète's infinite product: \begin{equation} \prod_{n=1}^{\infty}\cos\left(\frac{\theta}{2^n}\right)=\frac{\sin(\theta)}{\theta} \end{equation} For $\theta_1=\frac{8\pi}{7}$: \begin{equation} \frac{\sin(\theta_1)}{\theta_1}=\cos\left(\frac{4π}{7}\right)\cos\left(\frac{2π}{7}\right)... \end{equation} For $\theta_2=\frac{\pi}{7}$: \begin{equation} \frac{\sin(\theta_2)}{\theta_2}=\cos\left(\frac{π}{2\times7}\right)\cos\left(\frac{π}{4\times7}\right)... \end{equation} Combining those together: \begin{equation} \frac{\sin(\theta_1)}{\theta_1}=\cos\left(\frac{4π}{7}\right)\cos\left(\frac{2π}{7}\right)\cos\left(\frac{π}{7}\right)\frac{\sin(\theta_2)}{\theta_2} \end{equation}

Since $\sin(\theta_1)=-\sin(\theta_2)$ \begin{equation} \frac{\theta_2}{\theta_1}=-\cos\left(\frac{4π}{7}\right)\cos\left(\frac{2π}{7}\right)\cos\left(\frac{π}{7}\right)=x \end{equation}

\begin{equation} x = \frac{1}{8} \end{equation}

Answer 3

The three corresponding nodes in the unit radius tetradecagon (14-gon) can be regarded as the tops of three isosceles with top angle $\alpha = \frac{\pi}{7}$, due to the equal chords:

Summing the bases of these isosceles yields the 'radius' of the 14-gon:

$$ \color{green}{g} \color{black}{+} \color{blue}{b} \color{black}{+} \color{red}{r} \color{black}{ = 1}$$

But we also have that:

$$\begin{align}\cos\left(\color{blue}{ \frac{2\pi}{7} } \right) &= \color{green}{g}\color{black}{ \,\,\,+ \,\,\,\frac{1}{2}}\color{blue}{b} \\ \cos\left(\color{green}{\frac{4\pi}{7} } \right) &= -\frac{1}{2}\color{green}{g} \\ \cos\left(\color{red}{\frac{6\pi}{7} } \right)&= -\color{green}{g} \color{black}{\,\,\,- \,\,\,} \color{blue}{b}\color{black}{ \,\,\,- \,\,\, \frac{1}{2}}\color{red}{r} \end{align}$$

Adding these gives

$$\cos\left(\color{blue}{ \frac{2\pi}{7} } \right) + \cos\left(\color{green}{\frac{4\pi}{7} } \right) + \cos\left(\color{red}{\frac{6\pi}{7} } \right) = -\frac{1}{2}\left(\color{green}{g} \color{black}{+} \color{blue}{b} \color{black}{+} \color{red}{r}\right)= -\frac{1}{2}$$

Answer 4

One can use complex numbers to find the value of $$\cos\frac{2\pi}{7}+\cos\frac{4\pi}{7}+\cos\frac{6\pi}{7}.$$

Let $\omega=e^{\frac{2\pi i}{7}}=\cos\frac{2\pi}{7}+ i\sin\frac{2\pi}{7}.$ $\omega$ is a zero of $x^7-1=(x-1)(x^6+x^5+\dots +x+1)$. Since, $\omega\ne 1$, it is also a zero of the second factor. So,

$$\omega^6+\omega^5+\dots +\omega+ 1=0.$$

Using DeMoivre's Theorem and taking the real part of both sides, gives $$\cos\frac{12\pi}{7}+\cos\frac{10\pi}{7}+\dots +\cos\frac{2\pi}{7}+1=0.$$

Let $S=\cos\frac{2\pi}{7}+\cos\frac{4\pi}{7}+\cos\frac{6\pi}{7}$. Now, $$\cos\frac{12\pi}{7}+\cos\frac{10\pi}{7}+\cos\frac{8\pi}{7}=\cos(2\pi-\frac{2\pi}{7})+\cos(2\pi-\frac{4\pi}{7})+\cos(2\pi-\frac{6\pi}{7})=S,$$ by the identity $\cos(2\pi-\theta)=\cos\theta$.

Therefore, $$\cos\frac{12\pi}{7}+\cos\frac{10\pi}{7}+\dots +\cos\frac{2\pi}{7}+1=2S+1,$$

and $$2S+1=0.$$

So, $S=-\frac{1}{2}$.

Answer 5

To complete Tim Raczkowski's solution we will the address the second part of the problem. Using the identical notation as above, we have $$\cos(2\pi/7)\cdot \cos(4\pi/7)\cdot \cos(6\pi/7)=$$$$(\omega+1/\omega)(\omega^{2}+1/\omega^{2})(\omega^{3}+1/\omega^{3})/8=\omega(\omega^2+1)(\omega^4+1)(\omega^6+1)/8=$$$$(\omega^{13}+\omega^{11}+\omega^9+2\omega^7+\omega^5+\omega^3+\omega)/8=(\omega^6+\omega^5+\omega^4+\omega^3+\omega^2+\omega+2)/8=1/8$$ Q.E.D.