4

I have just begun to study complex analysis and I'm trying to calculate

$$ \int_{- \infty}^{\infty} \frac {\sin^3 x}{x^3} dx $$

with the "help" of an exercisebook.

I have followed these steps:

$$\int_{- \infty}^{\infty}\left( \frac {e^{ix}-e^{-ix}}{2i}\right)^3 \frac {1}{x^3} dx$$

$$\frac {1}{(2i)^3} \left(\int_{- \infty}^{\infty} \frac {e^{3ix}}{x^3} dx - \int_{- \infty}^{\infty} \frac {3e^{2ix}}{x^3}dx - \int_{- \infty}^{\infty} \frac {e^{-3ix}}{x^3}dx + \int_{- \infty}^{\infty} \frac {3e^{-2ix}}{x^3}dx\right)$$

The book says that

If we consider a bend path with radius $R\to \infty $ on the upper half-plane, the first and second integrals are equal to zero because the closed curve doesn't contain any singularity. But if we consider the inferior half-plane (and the corresponding half-circle driven clockwise), the path contains the singularity $x=0$.

But it was told me that $x=0$ isn't a singularity point because $ \lim_{x \to 0} \frac {\sin x}{x}=1 $.

Now, I can't undestand:

  • If $x=0$ is a singularity and why
  • Why the upper half-plane doesn't contain the singularity and why the inferior one does.

Many thanks for your help

Reading the the comments, I have made this sketch

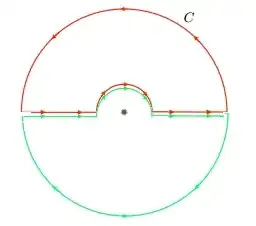
enter image description here

can you tell me if it is correct?

sunrise
  • 1,245
  • NB I corrected a typo in the first occurence of $\sin$. Made no $sen\text{se}$ the way it was ^^ – AlexR Nov 06 '14 at 20:28
  • 1
    $0$ is not a singularity of $\left(\frac{\sin z}{z}\right)^n$, but it is a pole of $\frac{e^{inz}}{z^n}$. It lies neither in the upper nor in the lower half-plane, or it lies half in each, but when the book says "if we consider a bend path", they probably mean a path with a small dent circumnavigating $0$ in the upper half-plane, so that you close the contour with a semicircle in the upper half-plane, the contour doesn't enclose the singularity, but if you close it in the lower, it encloses $0$. – Daniel Fischer Nov 06 '14 at 20:28
  • 1
    @AlexR In Spanish, the function is called "sen", so it does make sense (still, $\sin$ is of course righter). – Daniel Fischer Nov 06 '14 at 20:29
  • @DanielFischer Thanks for the enlightenment ;) – AlexR Nov 06 '14 at 20:30
  • @AlexR You're welcome. And: Écrasez l'infâme! – Daniel Fischer Nov 06 '14 at 20:32
  • @DanielFischer thanks for your answer. If you could add a sketch, I'd be sure to have correctly understood. Many thanks! – sunrise Nov 06 '14 at 20:43
  • 1
    Here is a picture with such a contour. – Daniel Fischer Nov 06 '14 at 20:48
  • @DanielFischer thanks! It seems "working".... but the half-circle of infinite radius is also on the inferior half-plane, but it is driven clockwise.. I'm sorry It wasn't clear in the question, I have corrected it. So I haven't understood... Can I make the small dent in the upper half-plane and not make it in the lower one? – sunrise Nov 06 '14 at 21:08
  • You can make the small dent in whichever half-plane you like. If you make it in the same half-plane as the large semicircle, then the contour doesn't enclose the pole, and if you make it in the other half-plane, the contour encloses the pole. – Daniel Fischer Nov 06 '14 at 21:16
  • 2
    See this solution http://math.stackexchange.com/questions/406939/fourier-transform-of-textsinc3-pi-t/407382#407382 Your case is the special case $u=0$. – Ron Gordon Nov 06 '14 at 21:25
  • @DanielFischer thanks. Can you tell me if the sketch is correct? – sunrise Nov 06 '14 at 21:52
  • @RonGordon many thanks for your comment!! I'm going to read carefully your link tomorrow morning.. now it's too late.. thanks again! – sunrise Nov 06 '14 at 21:57
  • Yes, that is how things look if you make the small dent around $0$ reach in the upper half-plane. – Daniel Fischer Nov 06 '14 at 21:57
  • @DanielFischer oh, thank you!!! If you write a little answer, I'll be happy to give you the "accepted answer" :) – sunrise Nov 06 '14 at 22:01
  • You could write one yourself tomorrow, after going through Ron's link to deepen your understanding. It helps strengthening your understanding to write it down. If you do a good job, I'll be happy to upvote. – Daniel Fischer Nov 06 '14 at 22:06
  • But if you don't want to write it up yourself tomorrow, you can ping me and I'd do it. – Daniel Fischer Nov 06 '14 at 22:09
  • @DanielFischer do you plan on writing an answer so those post can be marked solved? – dustin Jan 02 '15 at 00:37
  • @dustin I'm sorry! I'll do it this afternoon, at the moment I'm not at home! Have a nice day! – sunrise Jan 02 '15 at 09:52
  • @DanielFischer I have just written an answer, I'll be glad if you read it! :) Have a nice day! – sunrise Jan 02 '15 at 23:24

1 Answers1

1

We are in this situation: $$ \int_{- \infty}^{\infty} f(x) dx $$

but it is equivalent to $$ \lim_{R \to + \infty} \int_{- \infty}^{\infty} f(x) dx $$

Now we can consider the real case as a particular case of the complex case; so we can use the complex variable $z$ and consider the complex plane. We can write:

$$= \oint_C f(z) dz $$

So we want to close the path.. we can't have a straight line from $-R$ to $R$, because $z=0$ is a pole (a pole, not a singularity, because $ \lim_{x \to 0} \frac {\sin x}{x}=1 $) We can climb over the pole drawing a small half-circumference with infinitesimal radius $\epsilon$:

enter image description here

Considering that writing the sinus in exponential form, we have 2 exponential terms, one of them is positive and the other is negative, we have to consider both the two half-circumferences, and you can see that the upper one doesn't contain the pole while the lower one does.

I suggest you to also read this very interesting answer Fourier transform of $\text{sinc}^3 {\pi t}$

Community
  • 1
sunrise
  • 1,245