4

Prompted by a previous question found at Using a balun with a resonant dipole -- an answer there included the following text:

"For transmission lines (twin-lead or coax) to not radiate, each conductor must carry equal and opposite currents. It's these equal and opposite currents canceling each other that results in zero net field away from the transmission line. If the currents are not equal and opposite, then they don't cancel, and the difference results in an external electromagnetic field, and your transmission line radiates like an antenna."

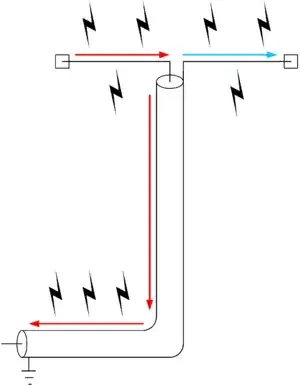
A sketch included in that link (repeated below), and the comments about it there are unclear as to how the common-mode r-f current flowing on a braided outer conductor of a perfectly terminated coaxial cable always is confined to the inner surface of that braid.

"Skin effect" keeps most of the r-f current flow very close to the surface of a conductor. But in a braided conductor, what prevents that current from being distributed ~ equally around the circumference of each unit conductor of that braid?

If it was/is, then wouldn't the outer surface of that outer conductor always be "hot" for r-f energy, just as are both conductors of twin-lead transmission line?

It is understandable that r-f current flowing on the inner surface of the outer conductor of rigid coaxial transmission line could not cross to its outer surface until functional paths existed for that purpose, usually at the load end of the line.

Isn't that also true when the outer conductor is braided, if that braid provides paths for r-f current to flow from the ID to the OD of the outer conductor along its entire length?

enter image description here

Richard Fry
  • 2,922
  • 7
  • 18

3 Answers3

1

A differential-mode current on the shield is always found exclusively on the inside surface of the shield, even if there are holes. It's not due to the current being trapped inside, but rather that it wants to be that way due to eddy currents, the same mechanism behind skin effect.

Imagine a primary current flowing through a solid, cylindrical conductor. Let's pretend it's a uniform current through the entire cylinder.

enter image description here

The primary current (straight red line) has an associated magnetic field (green circle). The right-hand rule determines the direction the magnetic field curls.

Because this is an AC current, that magnetic field is constantly changing. This in turn induces eddy currents (red circles) by Faraday's law of induction. The left-hand rule determines which way they go.

We can consider the net current we observe as the superposition of the primary and eddy currents. In the center of the conductor the eddy currents oppose and cancel the primary current, meaning very little net current in the center of the conductor. On the outside of the conductor the eddy and primary currents point in the same direction, so this is where most of the current is found.

Within the conductor, the eddy currents cancel the magnetic field. But the conductor is still surrounded by a magnetic field in space around it. And surrounding the space around the center conductor is the shield, which will intercept that magnetic field and thus have eddy currents induced within it.

enter image description here

Because we're talking about a piece of coax with only differential-mode current, we know there's an equal but opposite current in the shield, going down. Look now at the orientation of the eddy currents and the effect they would have on a downward current in the shield: current on the inside of the shield is reinforced, whereas current on the outside of the shield is cancelled.

This is why differential mode current is on the inside of the shield. It's not because it's "trapped inside" by skin effect. Rather, it doesn't want to get out. Eddy currents give rise to skin effect which describes a single conductor. When there are two conductors the interaction between them must be considered.

The tendency for currents in two nearby conductors in opposite directions to have the highest current density in the regions nearest each other is called proximity effect. We see this not only in coax, but also in balanced transmission lines and transformer windings:

cross section of a twin-lead transmission line

When the currents are in the same direction, the opposite occurs: the current density is highest in the regions furthest apart. This is why skin effect can't be circumvented simply by making a thicker wire from thinner, individually insulated strands.

It's because of issues like this I find the "skin effect" or "three conductor" explanation of coax unsatisfying. It leads to a mental model of demons trying to get out and wreak havoc, contained by a magic skin effect barrier. What if there are holes in the barrier, as in the braid? Do the ends need to be sealed? Instead I find it more intuitive to think of the equal but opposite fields of the shield and center currents cancelling each other. This leads to a better intuition about what's required to prevent coax from radiating, and it works with balanced transmission lines also.

Phil Frost - W8II
  • 51,701
  • 6
  • 88
  • 212
  • What prevents r-f current that is APPLIED to one point on the outer diameter of a solid wire making up part of the coax shield braid from being conducted by the surface of that wire around its circumference to appear on its opposite side? – Richard Fry Feb 08 '18 at 14:22
  • @RichardFry By opposite side you mean the inside? Skin effect. Electromagnetism isn't just a matter of electrons moving around in wires like tubes. You must also consider the associated fields. Those fields cause interactions that can reach across holes or gaps in the shield. In RF engineering the fields are often more relevant than the charges moving around in the wires. – Phil Frost - W8II Feb 08 '18 at 14:30
  • "By opposite side you mean the inside?" No, I mean the outside surface of the wire at a point on that outside surface opposite the point on that outside surface where r-f current was first applied to that wire. – Richard Fry Feb 08 '18 at 14:57
  • @RichardFry If I'm understanding correctly, nothing prevents that. If you manage to excite an RF current on some part of the outside of the shield, no matter how small, that excitation will propagate as a wave over the entire shield surface until it's converted to heat or electromagnetic radiation. – Phil Frost - W8II Feb 08 '18 at 15:02
  • _"If you manage to excite an RF current on some part of the outside of the shield, ..."_Isn't that exactly what happens when the shield of a coaxial cable is attached to a coaxial r-f connector plugged in to the r-f output connector of a transmitter? IOW, if the shield has r-f current on its ID, why does it not appear on its OD? – Richard Fry Feb 08 '18 at 15:20
  • @RichardFry No, that's not what happens. Connectors don't attach to the "inside" or the "outside" of the shield. Contrary to what you may have read, the inside and outside of the shield are not distinct conductors. You don't get to choose which to connect to. If an electron wants to move between the inside and the outside it's free to do so because the shield is made of metal and metal has high electron mobility. The eddy currents illustrated in the 2nd figure are one way to explain why the current density "wants" to be highest on the inside of the shield for a differential-mode current. – Phil Frost - W8II Feb 08 '18 at 15:44
  • 1
    Let us continue this discussion in chat. – Phil Frost - W8II Feb 08 '18 at 16:02
1

Is RF current always confined to the inner diameter of a braided outer conductor of coaxial cable?

Quick answer: No. And when it isn't, it's called common mode current. Common mode current is typically induced by external fields between the coax shield and other objects (like the antenna), rather than the RF current injected into the end of the cable.

Common mode current can be blocked by chokes/baluns, or discouraged by careful symmetrical arrangement of the coax and antenna.

user10489
  • 6,170
  • 1
  • 10
  • 23
0

Assuming decent coax that is properly terminated, and where the braid is not corroded and the strands are in good contact with each other, any small holes in the braid act like a waveguide below cutoff. Therefore, any radiation from the braid is usually inconsequential in amateur practice.

Having said that, in some cases there can be some radiation and/or some unwanted signal ingress. That's one of the reasons for double- and quad-shielded flexible coax (or solid shield coax).

Of course, if the unbalanced coax is connected directly to a dipole without a suitable balun, we will then have common-mode currents flowing on the outside of the shield. The shield will then radiate (as shown in the graphic) a significant signal, as well as pick up unwanted RFI, etc. whether the shield is braided or solid.

Mike Waters
  • 7,948
  • 4
  • 18
  • 51