RigExpert AA-35 - Interpreting The Information

Question

I have a new RigExpert AA-35 antenna analyzer. 1st one I have had & 1st time trying to use an analyzer on an antenna. My questions are very basic and general, but I am having difficulty in Googling for answers. Hope someone can help, or direct me to a document that would explain the meaning of these figures.

This analyzer produces many results when run. I understand the simple ones: Frequency, SWR, Return Loss, Wave Length. However there are several results, and some of those results that are presented in such a manner that I am not understanding what they are or what they mean. Here are the 10 main results that are shown when a test is run, along with an example of those results:

1. Freq in kHz = 511.2
2. SWR = 2.62
3. RL dB = 6.98
4. Z (Ohms) = 167.19 - j63.91
5. |Z| (Ohms) = 178.99
6. |rho| = .045, phase = 19.95 (Degrees)
7. C (pF) = 4871.47
8. Zpar (Ohms) = 191.62 - j501.28
9. Cpar (pF) = 621.08
10. 1/4 Cable Length = 317.47'

The results I do not understand are:

• Z (Ohms) = 167.19 - j63.91
• |Z| (Ohms) = 178.99
• |rho| = .045, phase = 19.95 (Degrees)
• Zpar (Ohms) = 191.62 - j501.28
• Cpar (pF) = 621.08

Here are my questions:

• Why for Z & Zpar are there 2 numbers, one with a j in front. What do those mean?
• What is the difference between Z & |Z| & Zpar?
• What is the difference between C & Cpar?
• What is rho?

Thanks in advance. At this time I am not looking for advice on this antenna itself, just on how I can interpret these figures.......

Answer 1

First, a general statement: the antenna analyzer has one set parameter, the frequency, and one measured parameter, the impedance (which is a complex number and therefore requires two real numbers to display).

Everything else can be derived, one way or the other.

Why for Z & Zpar are there 2 numbers, one with a j in front. What do those mean?

$Z$ stands for impedance, which is a complex number and so has to be written as made up of two real numbers. (Mathematicians write complex numbers with an $i$ instead of a $j$, but it means the same thing.) I won't explain complex numbers here — there's many different introductions and you should find one that makes sense to you.

Impedance is a quantity analogous to resistance which is useful in analyzing radio-frequency systems in the same way as resistance is useful in analyzing DC systems, and much of the math is the same; you just need to use complex arithmetic instead of real arithmetic.

Any time you see someone refer to the impedance of an RF device as, say, $50\,\Omega$, it's “really” $(50 + j0)\,\Omega$ — that is, the complex number has a zero “imaginary part” and since it is zero we can leave it out (after all, anything multiplied by zero is zero and adding zero doesn't change a number, so $50 + j0 = 50 + 0 = 50$.)

Impedance corresponds to resistance whenever the imaginary part is zero; when it's nonzero, that means the thing that has that impedance resembles an inductor or a capacitor (it can't be both) at that frequency. The imaginary part is called reactance. Reactance is like resistance except that instead of dissipating energy, it releases it later in some way.

• The impedance of an ideal resistor is always $(x + j0)\,\Omega$ for some $x$.
• The impedance of an ideal capacitor is always $(0 - jx)\,\Omega$ for some $x$.
• The impedance of an ideal inductor is always $(0 + jx)\,\Omega$ for some $x$.

When you get into more complex (and realistic) circuits, including an antenna at the end of a length of transmission line, both will be nonzero. (Or, a simple example: as you may know, if you put two resistors in series you add their resistances. The same implies to impedances: if you have an inductor with impedance $Z_L$ and a resistor with impedance $Z_R$ in series, the impedance will be $Z_L + Z_R = jx\,\Omega + y\,\Omega = (x + jy)\,\Omega$ for the particular $x$ and $y$.)

What is the difference between Z & |Z| & Zpar?

$|Z|$ is the magnitude of the impedance. Imagine you take the two parts of the complex number and use them to mark a point on graph paper; the magnitude is the distance from the origin (i.e. the square root of the sum of the squares).

I don't offhand remember what $|Z|$ is good for when analyzing antennas.

$Z_{\text{par}}$ should be the same as $Z$, I would think, because there's only one impedance value regardless of the model (see below for explaining "par").

What is the difference between C & Cpar?

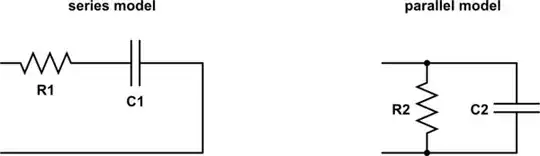
$C$ is capacitance, but the impedance (or reactance) of a capacitor is not only dependent on its capacitance, but also the frequency. But the analyzer knows the frequency being applied, so it can compute "If we assume the circuit under test is actually a resistor in series with a capacitor, what is the capacitance that would produce the observed impedance at this frequency?"

$C_\text{par}$ is the same, except that it is for the model of a resistor in parallel with a capacitor instead of in series.

If the analyzer displays $L$ values, they are the same except that the circuit is more like an inductor than a capacitor and it is displaying those values.

Answer 2

Welcome to StackExchange. Your questions are natural for a new user of an instrument like the AA-35. Some of your questions are addressed in the item on Impedance in Wikipedia.

Impedance, denoted as $Z$, describes two aspects of a circuit's behavior when stimulated with AC: resistance, $R$, which dissipates energy, and reactance, $X$, which stores and releases it as the AC stimulus fluctuates. In mathematical shorthand, these two aspects are combined into a single "complex" number: $Z_s=R_s+jX_s$, where the $s$ subscript denotes the series equivalent description of the impedance. More on that later.

$R_s$ and $X_s$ can be plotted on an $xy$-coordinate axis, with $R_s$ being plotted along the horizontal $x$-axis and $X_s$ along the vertical $y$-axis. The distance from (0,0) to the point ($R_s$,$X_s$) is the magnitude of the impedance,$|Z_s|$, which is calculated as: $$|Z_s|=\sqrt{R_s^2+X_s^2}$$ For the data in your question: $$|Z_s|=\sqrt{167.19^2+63.91^2}=178.99\Omega$$

We are perhaps most accustomed to describing the series equivalent impedance of an AC circuit - $Z_s=R_s+jX_s$ - but we may also describe it in terms of its parallel equivalent - $Z_p=R_p||X_p$. Knowing the series and parallel equivalents is useful when one wants to combine the measured circuit with other components, e.g., to match the measured circuit to a specific value.

Since series and parallel AC circuits behave so differently as a function of frequency, this transformation can only be accomplished at a single frequency. The essential nature of the transformation requires the Q of the series and parallel equivalents to be identical: $$Q_s=\frac{X_s}{R_s}$$ $$Q_p=\frac{R_p}{X_p}$$ equating $Q_s=Q_p$ and rearranging, $$R_p=R_s(1+Q^2)$$ $$X_p=X_s(1+\frac{1}{Q^2})$$

The parallel equivalent impedance, $Z_p$, is: $$|\frac{1}{Z_p}|=\sqrt{\frac{1}{R_p^2}+\frac{1}{X_p^2}}$$ which, of course, should equal $|Z_s|$.

Using the data in your question: $$Q_s=\frac{63.91}{167.19}=0.3822$$ $$R_p=167.19(1+0.3822^2)=191.6\Omega$$ $$X_p=-63.91(1+\frac{1}{0.3822^2})=-501.4\Omega$$ substituting into the equation for $Z_p$, $$|\frac{1}{Z_p}|=\sqrt{\frac{1}{191.6^2}+\frac{1}{501.4^2}}$$ $$|\frac{1}{Z_p}|=0.005587$$ so, $$|Z_p|178.98$$

The value of $C_{par}$ is calculated from the equation for capacitive reactance: $$X_c=\frac{1}{2\pi f C_{par}}$$ which is rearranged to provide $C_{par}$: $$C_{par}=\frac{1}{2\pi f X_c}$$ and, using the value of $X_p=-501.4\Omega$ obtained above, $$C_{par}=\frac{1}{2\pi\space 511.2kHz\space 501.4\Omega}=621pF$$

Though you did not mention SWR in your question, I note that the SWR reported in your question is correct only if the reference impedance, $Z_0$, is 75$\Omega$, so I will use that value throughout.

I confirmed with Rig Expert support that $\rho$ is the reflection coefficient, sometimes denoted by $\Gamma$: $$\rho=\frac{Z_L-Z_0}{Z_L+Z_0}$$ Remembering that $Z_0$ and $Z_L$ can be complex numbers - i.e., each can comprise resistance and reactance - $\rho$ can be stated as a complex number or in terms of its magnitude and angle. For the example given in your question, this online calculator gives: $$|\rho|=0.4478, arg(\rho)=-19.95^\circ$$ Note that the values you reported in your question are different, which bears re-checking. And, just for completeness, $$SWR=\frac{1+|\rho|}{1-|\rho|}$$ substituting from above: $$SWR=\frac{1+0.4478}{1-0.4478}=2.62$$

Answer 3

Nearly all of these things are just the antenna impedance, expressed a different way.

Why for Z & Zpar are there 2 numbers, one with a j in front. What do those mean?

Z represents impedance. It's essentially the concept of resistance, but extended to work for AC circuits. Impedance is a complex number, which consists of two parts. The first part is a real number, and is the resistance. The second part is an imaginary number which represents reactance, which accounts for the effects of things like inductors and capacitors. The j is the imaginary unit, which is just part of the notation for writing imaginary numbers.

What is the difference between C & Cpar?

One way to represent an impedance is to come up with an equivalent circuit made of resistors and capacitors that would have the same impedance (though only at the single frequency tested). That can be done as a series or a parallel circuit:

^{simulate this circuit – Schematic created using CircuitLab}

$C$ is the value required for the series circuit, and $Cpar$ is for a parallel circuit. The RigExpert doesn't give a value for the resistor, because that's just the first part of the impedance, either Z or Zpar for the series or parallel circuits, respectively.

In some cases you will see the rigexpert report $L$ and $Lpar$ instead, this means the capacitor should be swapped for an inductor.

What is the difference between Z & |Z| & Zpar?

$Z$ is just the resistance and capacitance of the series equivalent circuit above expressed in a different way. Rather than give the value of the capacitor (or inductor) required in farads (or henries), it gives the impedance, which is the resistance plus the reactance. Calculating the reactance of a capacitor is just some simple math:

$$ X = - {1 \over 2 \pi f C} $$

And likewise for an inductor:

$$ X = 2 \pi f L $$

Where:

• $X$ is the reactance, in ohms
• $f$ is the frequency, in hertz
• $C$ is the capacitance, in farads
• $L$ is the inductance, in henries

So taking $C$ and the frequency from your example:

$$ {1 \over 2 \pi \times 511200 \times 621.08 \times 10^{-12}} = 63.91 $$

Note how this is the 2nd part of $Z$.

Zpar is just the same thing, but with Cpar instead. I would note this notion of "parallel impedance" is a bit of mathematical nonsense specific to the RigExpert. Because impedance is a single number, just one impedance can't be arranged "in series" or "in parallel". Zpar does tell you the equivalent parallel resistance, and the reactance of the equivalent parallel capacitor, but adding these numbers together doesn't make sense because parallel impedances don't combine by adding. Rather, they combine like parallel resistors: the reciprocal of the sum of the reciprocals. And you will find the result of combining the equivalent components in parallel yields the (actual) impedance given as Z.

$|Z|$ is the magnitude of $Z$. Other terms for the same thing are the "modulus" or the "absolute value".

What is rho?

It should be the reflection coefficient, which is just yet another way to express an impedance, but which also takes into account a characteristic impedance which the RigExpert is going to assume is 50 or 75 ohms, depending on the settings.

From the numbers you've provided, it looks like your RigExpert is currently set to 75 ohms, and there was an error in transcribing the magnitude which should be 0.45, not .045.