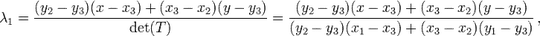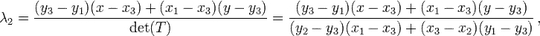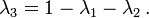Convert point to its barymetric coordinates

Question

I'm making a 2.5D game engine (in JavaScript) and I'm trying to get it to detect whether a block is under the cursor. This would be a simple task were it restricted to single-level isometric coordinates, but instead it's supposed to support isometric worlds, trimetric worlds and well, any projection angle really, in addition to it being multi-level (tiles can be stacked on each other up to an arbitrary limit). Almost all the conditions are arbitrary, but I've managed to narrow the problem to this, for now:

I need to know whether a point is inside a hexagon:

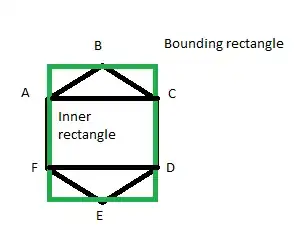
enter image description here

What I've set up so far is a bit hackish, I'm checking whether the point is inside the bounding rectangle first to drop out the most obvious cases. Next, I'm checking whether it's inside the rectangle formed by the points ACDF, another easy check. Now the hard part is that I need to check whether the point is inside the triangles. That's pretty straightforward if you have the barycentric coordinates, but I seem to have lost all the knowledge of how to obtain them.

Do take into account that while the inner rectangle is always a rectangle, the triangles might not be equal-sided. Bonus points if there's an optimization to be made because the bottom (or top, respectively) of the triangle is flat.

If you post a link to the image, someone with more rep can easily put the image inline. Uploading to imgur is a fine option. — House, Jul 31 '12 at 16:06

score 2 · Accepted Answer · answered Jul 31 '12 at 18:39

Wikipedia has an excellent article explaining exactly how to get the barycentric coordinates at 2.1 Converting to barycentric coordinates

From Wikipedia:

Explicitly, the formulae for the barycentric co-ordinates of are:

enter image description here

So in your top triangle A.x would correspond to x1, A.y to y1 and so forth. Plugging in the values in the formulae will yield the lamdas which are your barycentric coordinates. If they are all positive then the point is obviously inside the triangle.

Possible optimization due to the bottom of the triangle being flat (by that I assume it doesn't rotate or can be evaluated in local coordinates) is that one lambda can easily be evaluated by comparing only the y-values like:

lambda1 = y1 - y

Somehow I missed that part when reading the article, excellent, thanks!!! Posting my implementation in a bit. — quinnirill, Jul 31 '12 at 19:13

score 2 · Answer 2 · answered Aug 01 '12 at 04:41

If your goal is only to do point-in-hex tests (and you don't actually need the barycentric coordinates themselves), then your problem becomes much easier; you can simply look at the equations of your line segments and find the intercepts with the horizontal span containing your test point, then check whether it falls between the two ends.

For instance, if the coordinates of your points A, B, C are (Ax, Ay), (Bx, By) and (Cx, Cy) with (Ay=Cy and Ax < Cx and By < Ay, akin to your illustration - note that I'm pointing positive Y in the down direction!) then the line segment through A and B is defined by x=Bx+(Ax-Bx)*(y-By)/(Ay-By) (you'll never divide by 0 here because we explicitly said that By < Ay, and you can confirm that plugging in y=Ay and y=By gives the correct values of x); likewise, the line segment through C and B is defined by x=Bx+(Cx-Bx)*(y-By)/(Cy-By). Once you have those two lines, you can just test to make sure the x position of your test point is between the two segments' values at its y:

bool TestPointInHex(point pt, point A, point B, point C, point D, point E, point F) {
  if ( (pt.y < B.y) || (pt.y > E.y) || (pt.x < A.x) || (pt.x > C.x) )
    return false;
  if ( (pt.y >= A.y) && (pt.y <= F.y) )
    return true;
  if ( pt.y < A.y ) {
    float leftX = B.x + (A.x-B.x)*(pt.y-B.y)/(A.y-B.y);
    float rightX = B.x + (C.x-B.x)*(pt.y-B.y)/(C.y-B.y);
    return ( (pt.x >= leftX) && (pt.x <= rightX) );
  } else { // pt.y > F.y
    float leftX = E.x + (F.x-E.x)*(pt.y-E.y)/(F.y-E.y);
    float rightX = E.x + (D.x-E.x)*(pt.y-E.y)/(D.y-E.y);
    return ( (pt.x >= leftX) && (pt.x <= rightX) );
  }
}

Thanks! Seems a lot simpler. I'll try this one later, now I'll focus on trying to get stuff working with the current algorithm, replacing it later is trivial as the method takes no arguments and returns a boolean. :) — quinnirill, Aug 01 '12 at 08:24

score 1 · Answer 3 · answered Jul 31 '12 at 19:19

Thanks to @mikael-hogstrom 's answer, here's a function I created for the purpose:

/**
 * Checks whether point `p` is inside triangle `abc` based on barycentric
 * coordinates.
 *
 * @param {Number} px x of p
 * @param {Number} py y of p
 * @param {Number} ax x of a
 * @param {Number} ay y of a
 * @param {Number} bx x of b
 * @param {Number} by y of b
 * @param {Number} cx x of c
 * @param {Number} cy y of c
 *
 * @return {Boolean} A boolean indicating whether p is inside abc
*/
function isPointInsideTriangle (px, py, ax, ay, bx, by, cx, cy) {
        var v0x = bx - ax
        var v0y = by - ay
        var v1x = cx - ax
        var v1y = cy - ay
        var v2x = px - ax
        var v2y = py - ay

        var d00 = v0x * v0x + v0y * v0y
        var d01 = v0x * v1x + v0y * v1y
        var d11 = v1x * v1x + v1y * v1y
        var d20 = v2x * v0x + v2y * v0y
        var d21 = v2x * v1x + v2y * v1y

        var denom = d00 * d11 - d01 * d01

        var v = (d11 * d20 - d01 * d21) / denom
        var w = (d00 * d21 - d01 * d20) / denom
        var u = 1.0 - v - w

        return u >= 0 && v >= 0 && u + v < 1
}

I think I'll just optimize it later if necessary. :)

Here's a silly test page to try it in action: http://labs.avd.io/bary.html

Thanks to everyone for the help!

Convert point to its barymetric coordinates

3 Answers3