Gimbal lock occurs when your internal structure for storing/composing rotations uses a gimbal model:
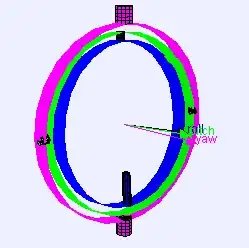
Image via Wikipedia, attributed: "By Lookang many thanks to Fu-Kwun Hwang and author of Easy Java Simulation = Francisco Esquembre - Own work, CC BY-SA 3.0"
That is, when you construct your orientation as a sequence of component rotations with their own persistent angle, composed together.
When you do that, the resulting axis that a component rotates around depends on where it sits in the composition sandwich, and how the other components are twisting its local frame of reference.
Your rotations don't need to be "global" or "local" per se, but rather "composed" where you track and update a persistent value for two or more separate rotations - in any coordinate space at all - then combine them together. The value of the outer one changes the effect of the inner one.
When you use Euler angles / Tait-Bryan angles, the gimbal model is almost automatic. It's built right into the coordinate conventions you're using.
For example, in Unity, a rotation formed with angles (pitch, yaw, roll) is equivalent to the following three-step composition:
Quaternion rotation = Quaternion.AngleAxis(yaw, Vector3.up) // Outer gimbal.
* Quaternion.AngleAxis(pitch, Vector3.right) // Middle gimbal.
* Quaternion.AngleAxis(roll, Vector3.forward); // Inner gimbal.
So if pitch is +- 90, then the inner gimbal's axis (local z) is turned until it's parallel to the outer gimbal's axis (parent y), and you have gimbal lock.
The angle triplet presentation misleads us into thinking these three angles are independent, like the three components of a translation vector. But they aren't truly. So if we store our rotation as 3 angles and add/subtract increments from them, they can eventually wander into a gimbal configuration where those increments do something very different than we intuitively expect!
Note that the gimbal lock is still there, even though we rephrased the multiplication in terms of quaternions. So that's the sense in which "quaternions don't avoid gimbal lock": they don't retroactively erase gimbals that you already baked into your model for how your application stores/updates its rotations.
But there is a sense in which quaternions do help avoid gimbal lock. That is: they don't make us construct our rotations from stacked yaw pitch and roll components, the way that Euler/Tait-Bryan angle approaches lure us into.
Instead of storing three persistent angles and adding to them separately (gimbals), we can store one persistent orientation and update it all at once.
Quaternion newWorldOrientation = oldWorldOrientation * localIncrement;
Now we're not relying on three separate angle variables (gimbals) tracking a persistent state. Our state is represented by a single quaternion, which treats all rotations uniformly - it is "gimbal-free".
Note that here, we sill have a combination of local and world rotations, but without creating gimbal lock.
We can do the same thing with Euler angles even - it's just a bit more convoluted:
// Encode the angles into a form that we can compose "gimbal-free".
oldRotationMatrix = MatrixFromEuler(currentEulerAngles);
// Do the composition as a whole, rather than one sequenced step per gimbal.
newRotationMatrix = oldRotationMatrix * localIncrementMatrix;
// Decode back to a (potentially very different) angle triplet.
currentEulerAngles = newRotationMatrix.eulerAngles;
We can even use angles to compute our local increment:
localIncrement = Quaternion.Euler( Input.GetAxis("Vertical") * -rotationSpeed * Time.deltaTime,
Input.GetAxis("Horizontal") * rotationSpeed * Time.deltaTime,
0);
Just note that here again, we're not storing a persistent yaw and adding/subtracting an increment to it each frame. Instead, we're composing-together just our incremental angle changes (which is reasonably safe since the increment on any single frame will be close to zero), then applying that change as a whole to our persistent rotation state - not composing it one gimbal at a time.
