Finding the position of a point inside a triangle, based on the position of a point in another triangle (barycentric coordinates in Godot)

Question

I'm trying to translate a UV coordinate into a world coordinate. (this is not in a shader, it's in GDScript in Godot, to bake out a texture based on some raycasts).

So I find out which triangle in the UV map the coordinate is in and then I find the corresponding triangle in the mesh and get it's world position, that's all good.

But then I can't figure out how to translate the points relative position inside the UV triangle to the mesh triangle.

I've been trying to use the distance from the point to each of the triangle points as weights to how much of each of the mesh points I should use to find the point I'm looking for, but having no luck.

Any help would be much appreciated.

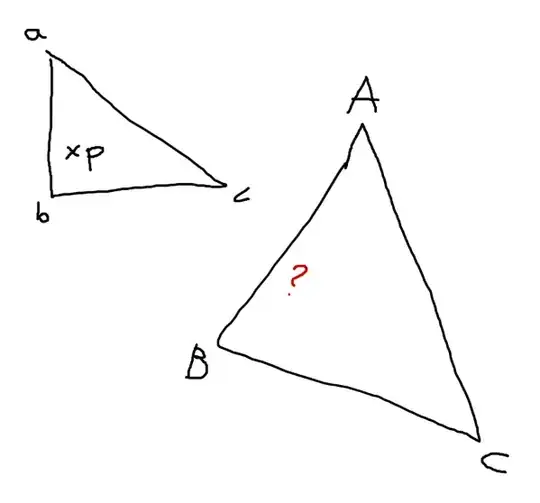
Not sure how best to illustrate this. But imagine you had a triangle where you knew the corner points a, b, and c, and a position inside it p. And you had another triangle where you knew the corner points A, B and C, how would you find a point that was relative in the same as p is to abc in triangle ABC.

EDIT: I added an answer based on the comments from DMGregory

It looks like you need Barycentric Coordinates. See What's the most efficient way to find barycentric coordinates? — DMGregory, Nov 12 '20 at 21:55
Well that looks doable. I just have to find an implementation I can figure out for going both ways and implement in GDScript. Thanks so much. — Kasper Arnklit Frandsen, Nov 12 '20 at 22:53
If you solve your problem, please post your solution as an answer below that can help other Godot devs (and tag your question with Godot so they can find it). Or, if you hit a snag translating this to GDScript, edit your question to clarify what step you need help converting. — DMGregory, Nov 12 '20 at 22:56
Will do. I'm having a bit of trouble finding a good example of converting barycentric to cartesian though. At least one I can easily parse. — Kasper Arnklit Frandsen, Nov 12 '20 at 23:22
Hint: barycentric coordinates are interpolation weights. Take a weighted average of your vertex positions, using the barycentric coordinates as the weights. — DMGregory, Nov 12 '20 at 23:31
Got it now. Understandable that it wasn't described anywhere when it was so straightforward. It seems to work perfectly except for some other unrelated error in my code with some of my triangles being in the wrong order. It's a bit too late for me to fix it now. So I'll finish it up tomorrow and post the GDScript solution. Thanks so much. — Kasper Arnklit Frandsen, Nov 12 '20 at 23:54

score 3 · Accepted Answer · answered Nov 13 '20 at 08:55

As DMGregory suggested, Barycentric Coordinates were indeed the solution. Since there are no built-in functions for converting Cartesian to Barycentric in Godot, I converted the c++ answer here What's the most efficient way to find barycentric coordinates? to GDScript:

func cart2bary(p : Vector3, a : Vector3, b : Vector3, c: Vector3) -> Vector3:
    var v0 := b - a
    var v1 := c - a
    var v2 := p - a
    var d00 := v0.dot(v0)
    var d01 := v0.dot(v1)
    var d11 := v1.dot(v1)
    var d20 := v2.dot(v0)
    var d21 := v2.dot(v1)
    var denom := d00 * d11 - d01 * d01
    var v = (d11 * d20 - d01 * d21) / denom
    var w = (d00 * d21 - d01 * d20) / denom
    var u = 1.0 - v - w
    return Vector3(u, v, w)
func bary2cart(a : Vector3, b : Vector3, c: Vector3, barycentric: Vector3) -> Vector3:
    return barycentric.x * a + barycentric.y * b + barycentric.z * c

score 0 · Answer 2 · answered Dec 02 '20 at 13:28

0

I just stumbled across this question and wanted to post my solution, which is a lot smaller and more efficient than Kaspers answer:

static func transfer_point(from : Basis, to : Basis, point : Vector3) -> Vector3:
    return (to * from.inverse()).xform(point)

from and to are the triangles represented as a Basis like this: Basis(x, y z). A basis is a 3x3 matrix.

answered Dec 02 '20 at 13:28

Jummit

311
1
6

Oh interesting I had no idea you could use Transforms for that. I might have to test that out. Is there a way to check whether a point is in a triangle as well with that method? Because I also need to that in my case, which I can easily do with the bariacentric coods. – Kasper Arnklit Frandsen Dec 04 '20 at 07:27
There is a Geometry function for that: https://docs.godotengine.org/en/stable/classes/class_geometry.html#class-geometry-method-point-is-inside-triangle – Jummit Dec 04 '20 at 08:03
Yeah but if I have to run that as well I assume it is doing something like the baryacentric coords under the hood and any efficiency gains are out the window with using the Transforms. – Kasper Arnklit Frandsen Dec 04 '20 at 12:35
I wouldn't be so sure about that. is_point_in_triangle looks a lot simpler and doesn't use baryacentric coordinates. Even if it did, doing the baryacentric calculation in GDScript uses a lot of variables and function calls, which makes it slower than C++. – Jummit Dec 04 '20 at 18:10

Finding the position of a point inside a triangle, based on the position of a point in another triangle (barycentric coordinates in Godot)

2 Answers2