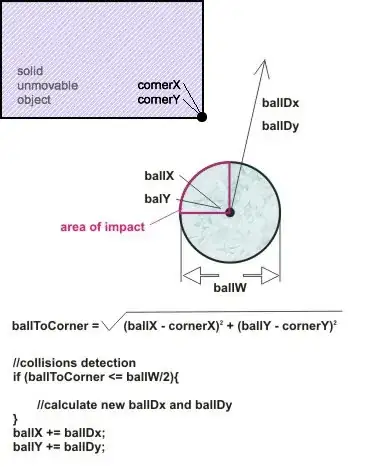
Note: All of the following assumes the ball's surface is frictionless (so it won't start spinning or rebound differently because it is).
At the moment of collision, the ball will be touching the corner. When solid objects collide, a force will act along the so called surface normal, i.e. perpendicular to the surface at the point of collision.
Since it's a ball, perpendicular to the surface is towards to ball's center. Ok, so we know the direction of the force, what about its magnitude? Assuming an elastic collision (and that the rectangle can't move), the ball must rebound at the same velocity it impacted with.
Let (nDx, nDy) be the velocity after collision, (oDx, oDy) the velocity before collision, and (x,y) the position of the ball at the point of collision. Let's further assume the corner the ball collides with is at (0,0).
Expressing our insights as formulae, we have:
(nDx, nDy) = (oDx, oDy) + c * (x, y)
length (nDx, nDy) = length (oDx, oDy)
Which is equivalent to:
nDx = oDx + c * x
nDy = oDy + c * y
nDx^2 + nDy^2 = oDx^2 + oDy^2
Substituting the first two equations in the last one, we get:
(oDx + c * x)^2 + (oDy + c * y)^2 = oDx^2 + oDy^2
Expanding using the binomial thorem
(a+b)^2 = a^2 + 2ab + b^2
yields:
oDx^2 + 2 * oDx * c * x + (c * x) ^ 2 + oDy^2 + 2 * oDy * c * y + (c * y) ^ 2 = oDx^2 + oDy^2
2 * oDx * c * x + 2 * oDy * c * y + (c * x) ^ 2 + (c * y) ^ 2 = 0
(2 * oDx * x + 2 * oDy * y) * c + (x^2 + y^2) * c^2 = 0
This quadratic equation for c has two solutions, one of which is 0. Obviously, that's not the solution we are interested in, as generally the direction of the ball will change as a result of the collision. To get the other solution, we divide both sides by c and get:
(2 * oDx * x + 2 * oDy * y) + (x^2 + y^2) * c = 0
That is:
c = -(2 * oDx * x + 2 * oDy * y) / (x^2 + y^2)
To summarize, we have:
c = -(2 * oDx * x + 2 * oDy * y) / (x^2 + y^2)
nDx = oDx + c * x
nDy = oDy + c * y
Edit: In code:
if (collision) {
float x = ballX - cornerX;
float y = ballY - cornerY;
float c = -2 * (ballDx * x + ballDy * y) / (x * x + y * y);
ballDx = ballDx + c * x;
ballDy = ballDy + c * y;
}
A few implementation considerations: While you can approximate (x,y) with the ball's position after the simulation step, this approximation will change the angle of deflection and hence be very noticeable, so your simulation steps need to be very fine (perhaps such that the ball doesn't move more than 1/20 of its diamater per step). For a more accurate solution, you could compute the time the collision occurs, and split that simulation step at that time, i.e. do a partial step until the point of collision, and another partial step for the remainder of the step.
Edit 2: Computing the point of impact
Let r be the radius, (x0, y0) the position and (dx, dy) the velocity of the ball at the beginning of the simulation step. For simplicity, let's further assume that the corner in question is located at (0,0).
We know:
(x,y) = (x0, y0) + (dx, dy) * t
We want
length(x,y) = r
That is
(x0 + dx * t) ^ 2 + (y0 + dy * t) ^ 2 = r^2
x0^2 + 2 * x0 * dx * t + dx^2 * t^2 + y0^2 + 2 * y0 * dy * t + dy^2 * t^2 = r ^ 2
(dx^2 + dy^2) * t^2 + (2 * x0 * dx + 2 * y0 * dy) * t + (x0^2 + y0^2 - r^2) = 0
\____ _____/ \____________ ___________/ \_______ ________/
\/ \/ \/
a b c
That is a quadratic equation in t. If its discriminant
D = b^2 - 4 * a * c
is negative, it has no solutions, i.e. the ball will never hit the corner on its present course. Otherwise, its two solutions are given by
t1 = (-b - sqrt(D)) / (2 * a)
t2 = (-b + sqrt(D)) / (2 * a)
We are interested in the time the collision started, which is the earlier time t1.
Your method would become:
// compute a,b,c and D as given above
if (D >= 0) {
t = (-b - sqrt(D)) / (2 * a);
if (0 < t && t <= ts) {
// collision during this timestep!
x = x + t * dx;
y = y + t * dy;
ts = ts - t;
// change dx and dy using the deflection formula
}
}
x = x + ts * dx;
y = y + ts * dy;