15

I'm interested in how this applies to higher numbers of dimensions too, but for this question I will focus solely on 2D grids.

I know that Perlin noise is not isotropic (direction invariant), and that the underlying square grid shows up enough to be able to identify its orientation. Simplex noise is an improvement on this but its underlying equilateral triangle grid is still not completely obscured.

My intuition is that any attempt to make noise of a particular frequency on a grid will result in a lower frequency in directions not aligned to the grid. So while attempts can be made to disguise this, the noise cannot in principle be isotropic unless it is generated without reference to a grid, allowing the average frequency to be the same in all directions.

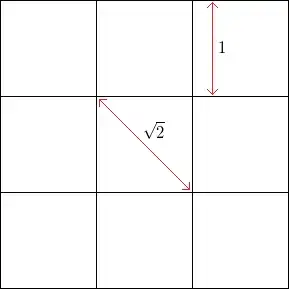
For example, with a square grid without noise, with square side length $n$, the frequency of vertices horizontally or vertically is $\frac1n$, whereas the frequency of vertices at 45 degrees (through opposite corners of the squares) is $\frac1{\sqrt{2}n}$.

Square grid showing length of edge and diagonal

Is there a random distribution that could be applied to offset the vertex positions that would result in the frequency becoming identical in all directions? My suspicion is that there is no such distribution, but I don't have a way of proving either way.

In short, is there a way of making perfect grid based noise of a given frequency, or should I be focused on other approaches (non-grid based noise or ways of disguising artifacts)?

ratchet freak
  • 5,950
  • 16
  • 28
trichoplax is on Codidact now
  • 6,292
  • 3
  • 23
  • 69
  • I think you might get a good answer from the signal processing or math site. – Alan Wolfe Aug 19 '15 at 01:01
  • 1
    I'm hoping that asking on computergraphics.SE will lead to answers that don't just give me signal processing theory or mathematical proofs, but the perspective of people who work with and research computer graphics. There may be something I haven't thought of that makes the question irrelevant, or it may only matter in certain circumstances, and if so I want the computer graphics angle on that. – trichoplax is on Codidact now Aug 19 '15 at 10:02
  • I've no idea how you would efficiently achieve random access to the final constructed data, nor how to extend it to 3D, but could you use something based on aperiodic tiling, e.g. https://en.wikipedia.org/wiki/Penrose_tiling ? i.e. have a random value at the centre of each tile? – Simon F Aug 19 '15 at 11:47
  • (caught by the edit period timeout) ...this was presuming you are concerned with more global alignment of the grid points and not just local effects. – Simon F Aug 19 '15 at 11:53
  • @SimonF I'm happy to use any kind of aligned grid (just a square grid would be fine) if a random offset can be applied to each vertex using a probability distribution that results in no grid aligned average frequency variations. I'd be interested to hear about another grid type if that makes the frequency isotropic - or any approaches that haven't occurred to me. My suspicion is that an aperiodic tiling, although globally isotropic, will be locally biased for any practical length scales. – trichoplax is on Codidact now Aug 19 '15 at 12:08
  • 1
    @trichoplax Another thought that occurred to me is that the displacements you're suggesting sound like the schemes used to approximate minimum distance Poisson disc distributions using a jittered grid, e.g as used for antialiasing. I believe some care is needed when choosing how to generate those jittered offsets. I tried quick search in my papers collection and one that sprang up is "Filtered Jitter", by V. Klassen, (http://onlinelibrary.wiley.com/doi/10.1111/1467-8659.00459/abstract). It's from 2000 so there may be better approaches, but it's surely worth a try. – Simon F Aug 19 '15 at 13:05
  • 2
    Here's an interesting paper: http://www.cs.utah.edu/~aek/research/noise.pdf (useful keywords: "Fourier spectrum") – John Calsbeek Aug 19 '15 at 14:39
  • @JohnCalsbeek I think that paper contains the makings of a great answer if you or anyone else wants to post it. – trichoplax is on Codidact now Sep 05 '15 at 15:24
  • @trichoplax One of the reasons that I haven't tried to write it up yet is that I don't see the anisotropy that you are talking about in any of the frequency domain images in that paper, so I feel like I'm missing something. – John Calsbeek Sep 05 '15 at 17:52
  • @JohnCalsbeek The first image shatters my intuition that Perlin noise would be heavily anisotropic, and shows that the problems are due to poor implementation and not really related to being grid based. I still don't have an understanding of why my initial intuition was so wrong. – trichoplax is on Codidact now Sep 05 '15 at 18:27
  • @trichoplax I can see directional artifacts in image 1b in that paper, even though the Fourier transform doesn't seem to show it. Unless that's what the extremely thin lines at right angles are? – John Calsbeek Sep 05 '15 at 21:45

1 Answers1

11

As usual with numerical methods and samplings, it also depends of your quality threshold of what you consider "isotropic". And of what you would consider as a being or not a "grid-based noise algorithm".

For instance Gabor Noise reproduces a target spectrum, for instance blue noise, which in Fourier domain is a simple isotropic ring. Now if you consider that this ring is not analytic but rasterized, as such it is not perfectly symmetrical. Also if the ring radius (i.e., frequency) get too close to the window size (i.e., maximum frequency), it will be truncated (and thus no longer symmetrical). Up to you to accept or not these as anisotropic ;-)

"this is not a circle" - Magritte "this is not a circle" - Nyquist "This is not a circle" - Magritte . . . . . . . . . . . . . . . . "This is not a circle" - Nyquist

You might or might not accept a rasterized ring in Fourier space to be "isotropic". Still, in the extreme cases where the ring get thinner than the resolution, or larger than the window, isotropy is objectively lost.

Community
  • 1
Fabrice NEYRET
  • 1,266
  • 8
  • 14