Electrons, as we all know, are incredibly small. Smaller things do tend to move faster, right? So exactly how fast considering how small they are? Also, does the electonegativity difference between two atoms alter the speed of the electron?
-
What do you mean by electonegativity between two atoms? – Mithoron Feb 22 '15 at 21:19
-
Electronegativity is the tendecy to attract shared elecrtons toward itself. I was wondering if an electron is being pulled between 2 atoms, would that alter its speed? – David Johnson Feb 22 '15 at 21:22
-
So you mean electronegativity difference - you should edit this. Electrons are very fast, but rater because of their low mass than size. – Mithoron Feb 22 '15 at 21:34
-
3about (1/137)c for hydrogen atom ground state. I'd write an answer but there is already a good one here: http://physics.stackexchange.com/questions/20187/how-fast-do-electrons-travel-in-an-atomic-orbital – DavePhD Feb 22 '15 at 22:50
-
A mind boggling 7.8 million kilometers per hour. – Pritt says Reinstate Monica Jul 12 '17 at 03:50
-
1 mm per second in Uranium atom. – junket Nov 26 '22 at 06:01
4 Answers
The ratio of the speed of an electron traveling in the first Bohr orbit to the speed of light is given by the handy equation
$$V_\mathrm{rel}=\frac{[Z]}{[137]}$$
where $Z$ is the atomic number of the element under consideration and 137 is the speed of light in atomic units, also known as the fine structure constant. Consequently a 1s electron in the hydrogen atom will travel at approximately 0.7 % the speed of light. In silver ($Z=47$) the 1s electron will travel around 34 % the speed of light, while the 1s electron in gold ($Z=79$) will travel at about 58 % the speed of light.
Once we get up to around silver, the electrons are traveling at relativistic speeds and this can dramatically impact properties of the atom. For example, the relativistic mass of an electron is given by
$$m_\mathrm{rel}=\frac{m_\mathrm e}{\sqrt{1-(V_\mathrm{rel}/c)^2}}$$
where $m_\mathrm{e}$, $V_\mathrm{rel}$ and $c$ are the electron rest mass, the velocity of the electron, and the speed of light respectively. The following figure provides a graphical representation of how the electron mass increases as the electron velocity increases.
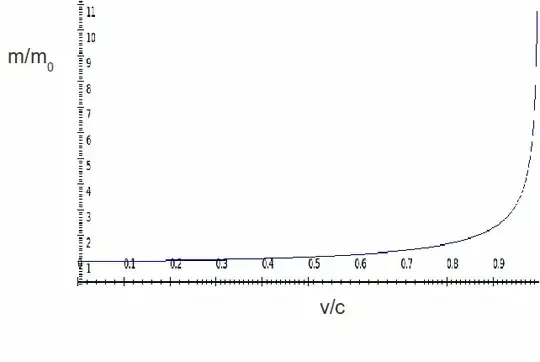
The following equation relates the ratio of the relativistic radius of the first Bohr orbit $R_\mathrm{rel}$ to the normal radius $R_0$, to the relativistic velocity of the electron
$$\frac{[R_\mathrm{rel}]}{[R_0]}=\sqrt{1-(V_\mathrm{rel}/c)^2}$$
As the relativistic velocity of the electron increases, the orbital radius contracts (the above ratio becomes smaller). For silver, the first Bohr radius contracts ~6 %, while for gold the contraction is ~18 %.
Look at these earlier Chem SE answers to see the interesting physical effects that atoms can exhibit when their electrons travel at relativistic speeds.
-
Just to add the importance of relativistic effects when you move down to heavier elements, DFT calculations on heavier atoms need to consider this relativistic effects when computing the electronic properties of molecules (materials), and can lead to interesting effects when included. I would highly recommend reading about Topological Insulators if you need a full physics description of why is it so. – Hemanth Haridas Nov 26 '22 at 16:54
Well, if you consider the ground state of hydrogen atom (Bohr's model), you can calculate the speed by using
$$\frac{m_ev^2}{a_0}=\frac{1}{4\pi \epsilon}\frac{e^2}{{a_0}^2}$$
You get
$$v=e\sqrt{\frac{1}{4\pi \epsilon m_ea_0}}$$
Plugging these values, you get speed to be approximately 2187691.264 m/s, or in other words, 7.8 million kilometers per hour.
It's pretty fast, especially for something thats stuck within a volume of $6.21×10^{-31} m^3$. In fact, at this speed, the electron could, in fact, circumnavigate the globe in 18.4 seconds! Pretty mind-boggling I guess.
- 8,708
- 5
- 43
- 93
If they actually moved in tight orbits, electrons would continuously radiate energy until they fell into the nucleus. Niels Bohr postulated that there were somehow stable orbitals and "ignored" the motion, the beginning of quantum theory (along with Einstein's work on the photoelectric effect). See Bohr model.
When an electron is accelerated (or decelerated), as opposed to staying in one orbital, it emits bremsstrahlung (see Bremsstrahlung).
- 32,365
- 1
- 35
- 69
-
Bohr didn't ignore motion - in his model orbits were circular, and haven't introduced orbitals. – Mithoron Nov 04 '16 at 18:00
-
1The point is that a circular - or any - orbit would continually radiate energy until the electron fell into the nucleus. Bohr was forced to sidestep that issue. – DrMoishe Pippik Nov 06 '16 at 01:07
The electrons do not move around the nucleus. Furthermore, they don't have a velocity. But they have a kinetic energy, which is not $1/2 mv^2$. This apparent paradox is explained by quantum mechanics. This theory will not be developed here, because it's too long. It would require a lot of pages !
- 28,241
- 3
- 29
- 61