Gravity inside a star?

Question

Recently, I answered this question and need some clarification regarding the gravity when within the radius of a star. I thought that, when something is inside a star (ignoring drag), it will experience less gravity because as it goes deeper inside, more and more mass is outside (in the up direction) the distance left before it reaches the center. Is this true, and is there a formula that needs certain parameters to calculate it?

Answer 1

If you consider a radially symmetric mass distribution, the gravity experienced at a distance $R$ from the center is caused by the mass inside the sphere with radius $R$, thus the mass $$M(R) = \int_0^R \varrho(r) 4 \pi r^2 dr$$ In a radial-symmetric case one can show that the contribution of all masses outside $R$ cancel each other.

Thus the experienced gravitational acceleration at radius $R$ is $$g(R) = \frac{G}{R^2}\int_0^R \varrho(r) 4\pi r^2 dr$$

The interesting part here is to know the radial density variation $\varrho(r)$ inside your body, thus the Sun in this case. This depends on the equation of state of the matter - which in turn is one of the least well known equations. Deriving that requires intricate modelling of the Sun. There are at least two nice answers which give the radial density variation. There's a link in the first answer to data for the standard solar model for radius, density, enclosed mass etc.

EDIT to add a way to address the density profile:

One may try to get a handle on the density by assuming a polytropic model for the star, such that the relation between pressure $p$ and density $\varrho$ reads like $$ p = K \varrho^\frac{n+1}{n}$$

With a constant $k$ and the polytrope index $n$. This is a result of the solutions of the Lane-Emden equation $$\frac{1}{\xi^2} \frac{\mathrm{d}}{\mathrm{d}\xi} \left(\xi^2\frac{\mathrm{d}\theta}{\mathrm{d}\xi}\right) + \theta^n = 0$$which is a dimensionless form of the Poisson equation for a radially-symmetric self-gravitating polytropic fluid, thus where density follows a function of the form $\varrho = \varrho_c \theta^n$ with a central density $\varrho_c$. This equation can be solved exactly for polytrope index 0 (isobaric polytrope), 1 (isothermal polytrope) and 5 (limited use as it results in infinite stellar radius) and can be addressed analytically via convergent series and can also be solved numerically for a wide range of cases.

Yet a main sequence star is believed to be around $n=3$ for the radiation zone. Fully convective stars follow more an adiabatic gradient with n = 5/3 being the ratio of the heat capacity at constant pressure and heat capacity at constant volume for an ideal mono-atomic gas. You will have to integrate the equation numerically for these cases, though.

(Reinhard Meinel gives excellent lectures on relativistic astrophysics - and I still use my notes from back then as reference - but I'm sadly not aware of any published form of the notes on this particular topic... maybe this)

Answer 2

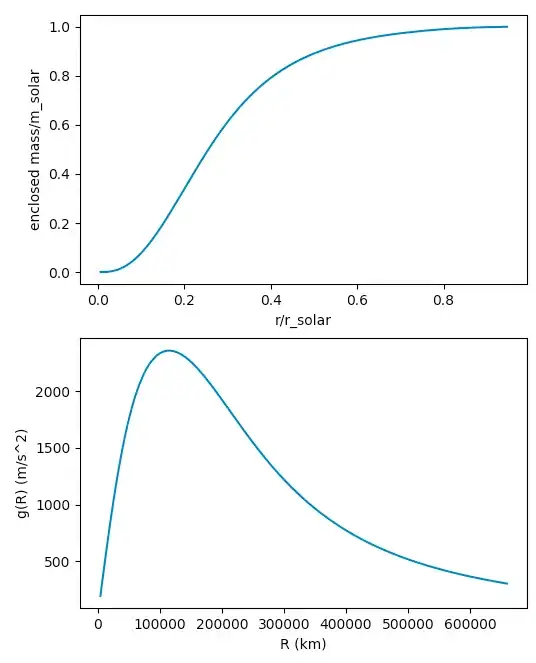
Just for fun I'll plot the data cited in @planetmaker's answer and use the equation there to plot the gravity.

We'll apply Newton's shell theorem to their equation:

$$g(R) = \frac{G}{R^2}\int_0^R \varrho(r) 4\pi r^2 dr = \frac{Gm(R) }{R^2} $$

where $m(R)$ is the mass enclosed by a sphere of radius $R$.

I plotted using this script.

It prints out 31.1 standard Earth gravities at surface which is close to Wikipedia's 28 Earth gravities. I didn't use interpolation or numerical integration or even Simpson's rule, so a 10% error is not surprising.

import numpy as np
import matplotlib.pyplot as plt
G = 6.67430E-11 # m^3/kg/s^2
data = [[float(x) for x in line.split()[:2]] for line in table.splitlines()]
m, r = np.array(data).T
r_solar, m_solar = 696342000., 1.9885E+30 # meters, kilograms
r_real, m_real = r * r_solar, m * m_solar
g = G * m_real[1:] / r_real[1:]**2
print(g[-1]/9.815, 'standard Earth gravities at surface')
plt.figure()
plt.subplot(2, 1, 1)
plt.plot(r, m)
plt.xlabel('r/r_solar')
plt.ylabel('enclosed mass/m_solar')
plt.subplot(2, 1, 2)
plt.plot(r_real[1:]/1000., g)
plt.xlabel('R (km)')
plt.ylabel('g(R) (m/s^2)')
plt.show()

using the copy pasted text of the table from here as table.

Answer 3

Yes. Insofar as such thing might be possible (perhaps in the style of the novel “The Mote in God’s Eye”), and assuming a star that has a spherically symmetrical mass distribution:

Gravity inside a star acts like if all the stuff in the shell of matter farther from the star’s center than you wasn’t there at all. You feel attraction only from the stuff “beneath you” (the inside sphere of mass closer to the star’s center than your ship). This result is typically proven via Gaussian surfaces.

To paint a mental picture: on an idealized Earth you feel exactly zero gravity from the atmosphere everywhere on the planet, and all the gravity force comes from the ground underneath your feet.

So the formula is the same Newton’s gravity formula and you only need to know the mass density function of the star (which by necessity of the spherical symmetry assumption must depend only on the distance to the star’s center). You integrate that density function from 0 to your ship’s distance from the star’s center, so you know what $M_1$ to plug into Newton’s gravity equation.

Notice that the spherical symmetry is vital to this result. If the mass density of the star is not spherically symmetrical, the Gaussian surface argument doesn’t hold and you are going to have to integrate the gravity equation for the whole star (below and above you) to find out.

(Also of course we assume that the star is not so dense and close that General Relativity starts to become important)

Answer 4

For an atom of mass $m$ in the sun to be at a constant radius $R$, the centrifugal force due to any non-radial thermal velocity component $v$ must be equal to the gravitational force, i.e.

$$m\frac{v^2}{R} = \frac{Gm}{R^2}\int_0^R \varrho(r) 4\pi r^2 dr$$

Assuming an isothermal gas ($v=const.$), this requires obviously a radial density distribution $$\varrho(r) \propto\frac{1}{r^2}$$

This is assuming a collisionless gas ball (undisturbed orbits of the atoms) and may therefore not be a particularly realistic model for a star, but it is interesting that this leads to the same radial density distribution $1/r^2$as the condition of hydrostatic pressure equilibrium for an isothermal ideal gas sphere

$$\frac{1}{\varrho(R)}\frac{dP(R)}{dR}= \frac{kT}{\varrho(R)}\frac{d\varrho(R)}{dR} = \frac{Gm}{R^2}\int_0^R \varrho(r) 4\pi r^2 dr$$

The gravitational force in this case is $\propto 1/R$.

Any temperature dependence on $R$ would obviously change the result.