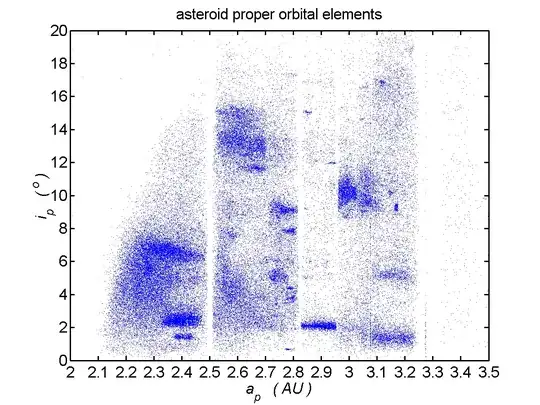
Short answer: The scarcity of asteroids with an inclination near zero is an expected result of normally distributed inclinations in 3-dimensions about the normal vector to the reference plane, rather than selection bias or an orbit "clearing" around zero degree inclination.
Long answer: Orbital inclination is typically defined as the angle between a reference plane and the orbital plane:
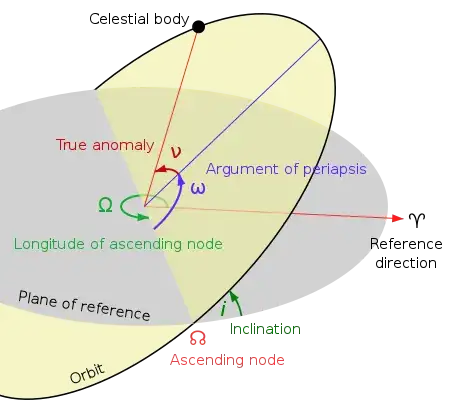
An equivalent definition is the angle between a reference plane normal and the axis of revolution of the orbiting body overlay-ed here:

Notice that the axis of revolution can be mapped to a point on the Celestial Sphere. We can generate a Gaussian distribution of points on the unit sphere centered with mean at the reference normal using the von-Mises Fisher distribution. The specific algorithm for generating sampling points is given on Stack Overflow.
Here is a group of 20 revolution axis intercept points with their corresponding circular orbits:
We can generate and plot a thousand points on a unit sphere (that I rotate to show the structure):
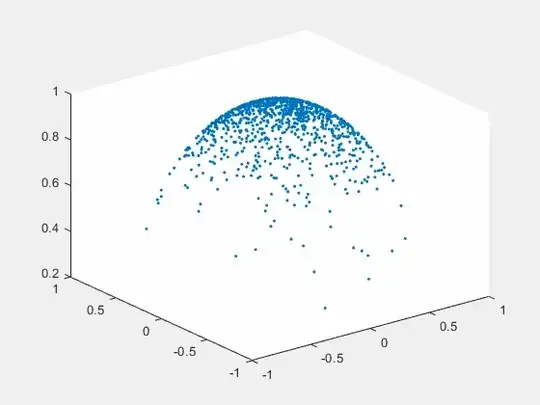
Note that only the very top points of this distribution correspond to inclination angles of nearly zero. As the inclination increases, the points get less dense, but the areas on the unit sphere are larger. The below plot is looking down from above the North Pole, with the orbits with inclination less than 2 degrees colored red, and the orbits with inclinations between 2 and 4 degrees colored green. Note that even though the points are the most dense at the pole, the area covered is the smallest, so 13 points are red, while 50 points are green. This is the explanation for why we see very few asteroid orbits with inclinations of less than 1/2 a degree from the original question.
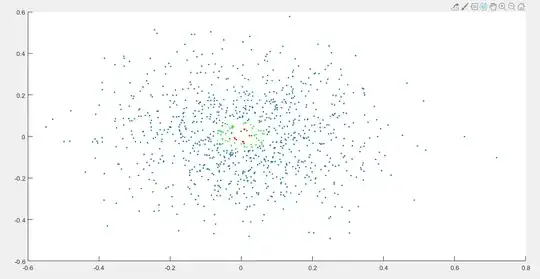
Below is a plot with the y-axis as inclination and x-axis as longitude compared with the OP's post. I chose a standard deviation that was much too large, but the 1000 point Monte Carlo demonstrates the same statistical effect asked about by the OP.

Notes:
The above example is for circular ellipses all with the same SMA for convenience, but I don't think we lose any generality.
I assume the reference plane in the picture used by the OP is the Earth's ecliptic, but the above answer works for the Sun's equatorial plane, or Jupiter's orbital plane, or any other close reference plane. We can assume that the asteroid inclination distribution 2D mean is actually going to be a bit offset from any choice of reference plane normal.
Orbital Mechanics can be very non-intuitive. Inclination is a 1D value, but its representative underlying probability distribution is best modeled on a 2D spherical surface in 3D.
It's somewhat ironic that I claim this is strictly a math problem, but there are no equations in the above post. The power of the Monte Carlo approach is in its simplicity and resultant appeal to mathematical intuition.
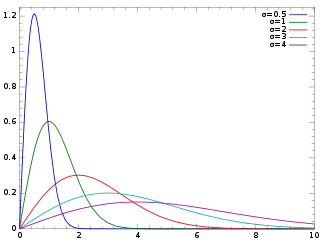
Statisticians/Probabilists should immediately recognize the distribution of orbit inclinations as a variant of the Rayleigh distribution which should lend a hint that a compression from 2D variables to 1D has occurred.
- My Matlab code is available on request.