9

I'm not asking about theoretical ball, vs saddle, vs flat surface which is just a metaphor with 2D space.

It's hard to say as we see very little of it, and we see them in the past because light travels for so long. But what we do know is that it is inflating (not exploding as one might thing from the "big bang" naming).

How would the universe look like, if we were to freeze it in a moment, is it likely to be a ball, or rugby ball, a cone or a sort of an irregular shape?

Is it filled throughout with galaxies, dust, black-holes, or does it live on the edges of its 3D shape, and the central part is "empty"?

Does it have a giant black hole or a star in the middle around which everything revolves?

Ska
  • 479
  • 3
  • 13
  • 3
    This question is confused, because it depends on some private notion of "geometric shape" that's not made clear. The geometric shape of the universe at any moment of cosmological time is flat, and that's not "just a metaphor with 2D space." Or rather, the bit of it we see is pretty flat, so if some version of the Copernican principle is assumed, then it is shaped like standard Euclidean $3$-space. If it's not assumed, then no answer to large-scale geometric shape can be given. – Stan Liou Jan 04 '14 at 13:01
  • 1
    OK, if it is shaped like "standard Euclidian 3-space", what kind of shape would it have? – Ska Jan 04 '14 at 16:12
  • 3
    Well, it is indeed flat, meaning Euclidean geometry can be used. Since light travels at a finite rate and the universe is not infinitely old, our 'bubble' of observable stuff within the universe would be in the shape of a sphere centered on us. However, the center of the sphere would change if you decided to move to a different part of the universe. Is the universe infinite? This is not known, since we cannot see passed our observational horizon. – astromax Jan 04 '14 at 16:52
  • .. Nor can we travel sufficiently far away to test this, I should add. – astromax Jan 04 '14 at 16:58
  • So, it is the limitation of our observation preventing us to even imagine the entire universe, i.e. beyond observable universe? I totally understand that observable universe is 3D space centred on us because of expansion, and that we perceive it as spherical. But can't we draw any conclusions about how the entire thing would look like? At least if we do assume it's a 3D space that's expanding, we could maybe dream up some possible shapes, unless a 4th dimension is in order, no? – Ska Jan 04 '14 at 20:52
  • @Ska: of course we can imagine different things beyond the horizon, but none of them have, or even could have, observational evidence for regions beyond the horizon. All we really know is that the part that we see is close to flat on average. To conclude any particular geometry beyond the horizon requires some assumption, such as the aforementioned Copernican principle. – Stan Liou Jan 04 '14 at 21:30
  • 2
    Possible duplicate of What is in the center of the universe? – James K Jul 29 '16 at 08:01

2 Answers2

6

Ok, maybe you have some misconceptions.

The Universe has no center at all. It looks the same from avaery point, to wherever you look to. It is approximatedly as follows:

Density filaments

This image represents a very large scale box on our universe on current time (not on perceived time, based on received light). Of course, it is just a computer simulation. Each dot represents a cluster of galaxies.

So you need to imagine an infinite tridimensional space filled with filament-like structures like these. And infinite means it has no bounds, so it has no "external" shape. No ball, rugby-ball nor cone there. Also not irregular external shape, just infinite. Any of these shapes have a 2D boundary on a 3D space, but the universe has no boundary.

Envite
  • 4,582
  • 12
  • 22
  • Where is this simulation from and where in it would be a Milky Way approximately? From this model it looks very much like cube-like shape, not infinite at all, not at this point in time at least. Maybe it can be considered infinite based on the speed of inflation: http://curious.astro.cornell.edu/question.php?number=575, but at any one given frozen point it is not. And although from the outside there is no spacetime, so no shape, we still "know" that galaxies put together, no matter how huge, are put together in a certain pattern, forming a certain "shape". – Ska Jan 04 '14 at 00:54
  • 3
    Being infinite doesn't imply having no boundary (not by itself, at least). @Ska: if you were looking for the distribution of galaxies, you should have asked for that directly. – Stan Liou Jan 04 '14 at 13:16
  • 1
    By the way, this box that people use to run simulations in is periodic (particles which go off one side appear on the other). @Ska The fact that they've chosen a cube to represent a chunk of the universe which they care to learn about is irrelevant. Also, that the universe is "infinite" is not something anyone can prove. The expansion of space-time seems to occur everywhere, but that does not mean that the universe is infinite. – astromax Jan 04 '14 at 16:57
  • @StanLiou: I'm interested in that too, but mostly about the outer shape of universe were it to freeze in time. – Ska Jan 04 '14 at 17:09
  • @Ska: based on what we know of gravity, space having a boundary is unphysical, so it probably doesn't have an "outer shape" at all. If you don't mean a boundary, then I'm afraid that I have no idea what you mean by "outer shape". – Stan Liou Jan 04 '14 at 18:47
  • @StanLiou: Not sure if I'm equipped with enough terminology, but assuming universe was very small in the very beginning, it did have a boundary. 0.00000000000000001 seconds later it was bigger, but it did have a boundary and a shape. 1M years later it was even bigger, and 13B years later it is roughly where it is now, I'm assuming that small atom like structure expanded into something that has a boundary and a shape too, just much bigger. – Ska Jan 04 '14 at 19:39
  • 1
    @Ska: your assumption is mistaken; space does not have and never had a boundary in any cosmological model consistent with what we know of gravity (the caveat is that our knowledge of gravity in the very early universe is completely uncertain). However, there was (and is) a horizon that defines the limit of possible observation, as astromax said above. But there's nothing physically special there; every point in space has its own horizon. – Stan Liou Jan 04 '14 at 20:07
  • @StanLiou: I can only imagine something like this in 4D, not 3D, if I take the analogy with inflating balloon and ants, and up it by 1 dimension, then I can understand this edge-less thing. But what is this 4th dimension then? Is this not then against Euclidian 3D space? I'll followup on observable universe point in astromax's comment. – Ska Jan 04 '14 at 20:47
  • @Ska: it isn't anything, because the geometry at hand is intrinsic and doesn't require being embedded in any higher-dimensional space. And the balloon analogy is only appropriate for one of the four possible homogeneous and isotropic spatial geometries. So no, it is not an argument against the possibility of Euclidean 3D space. – Stan Liou Jan 04 '14 at 21:35
  • @StanLiou: So something as hypertorus that can be expending, 3d, "flat", and still edge-less to the observer coming from our limited point of view and limited horizon? Why does it have to be repetitive though? If we really don't have means of testing, why repetitive, why not a ball with edge that's expanding so fast we'll never be able to reach it anyway. – Ska Jan 04 '14 at 21:53
  • 1
    @Ska: Yes, a flat $3$-torus is a possible geometry, but the geometry does not have to be "repetitive" in the sense of wrapping around on itself. It doesn't have to be a torus. Beyond the horizon could be a Euclidean space instead of a flat torus. Or there could be pink unicorns. Or anything else. The point of the horizon is that we don't know what's beyond it. (But if one assumes that the universe is globally isotropic, then it can't be a torus.) – Stan Liou Jan 04 '14 at 22:03
  • @StanLiou: So it seems like it boils down to this: It's probably flat, probably 3D. It might be edge-less, or not, we don't know. If yes, might be hypertorus and we could eventually do a round trip and came to starting point. If not, might be a ball, or anything else. We don't know, and can't imagine because of our limited scope. Is this at least remotely aligned with today's theories or are there still some gapping holes? – Ska Jan 04 '14 at 22:11
  • let us continue this discussion in chat – Stan Liou Jan 04 '14 at 22:16
4

The overall geometry and topology of the universe has been investigated by the Planck mission. Some results are described in this paper. Final results are not yet available.

An excerpt:

We have calculated the Bayesian likelihood for specific topological models in universes with locally flat, hyperbolic and spherical geometries, all of which find no evidence for a multiply-connected topology with a fundamental domain within the last scattering surface. After calibration on simulations, direct searches for matching circles resulting from the intersection of the fundamental topological domain with the surface of last scattering also give a null result at high confidence ... Future Planck measurement of CMB polarization will allow us to further test models of anisotropic geometries and non-trivial topologies and may provide more definitive conclusions, for example allowing us to moderately extend the sensitivity to large-scale topology.

The amount of anisotropy of the universe is going to be inferred from the cosmic microwave background (CMB).

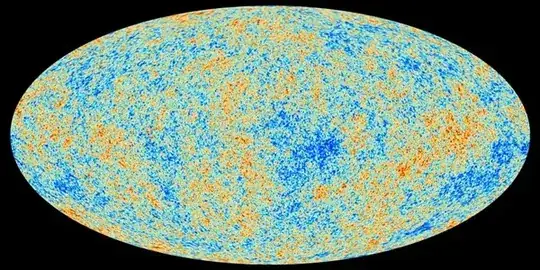
Cosmic microwave background, as inferred from the Planck data, Image Credit: European Space Agency, Planck Collaboration

Image Credit: European Space Agency, Planck Collaboration

Higher resolved images of the CMB can be found here

The universe is roughly a 4-dimensional spacetime with the big bang as a singularity. It has no edges in the 3d space when travelling. When looking to the past the border, if you like to call it like this, is the big bang. The big bang looks to us on Earth like being in a distance of 13.81 billion (13.81e9) light years in any direction. Or being 13.81 billion years in the past as light needed that time to travel to us. But we cannot travel to that boundary, because the universe expands faster than we (or light) can travel. We had to travel into the past or faster than light to get there, no matter in which spacial direction.

There is no black hole in the center of the universe, but the big bang, if you like to call it the center of a 4-d spacetime.

The universe, when looking to a fixed age of say 13.81 billion years is filled almost homogeneously with galaxies on the very large scale. Locally galaxies are grouped to clusters and superclusters. Superclusters form kind of a 3d-net. But there aren't totally void regions. There is always some gas or some dust or some plasma or some fast-travelling cosmic rays, neutrinos, etc.

If you could stop the expansion of the universe at a given cosmic time, you would see yourself in either direction in approximately the same distance, and in approximately the same past. (Such a structure is called a 3-sphere. The surface of a 4-ball is an example of a 3-sphere. This youtube video tries to visualize a rotating 3-sphere.)

Due to the fast expansion of spacetime, light cannot travel fast enough around the universe to make this possible. Therefore we can at best look back to the big bang, no matter which direction we look. The light needs more time to travel around the universe as the universe is existing after the big bang.

Gerald
  • 11,600
  • 27
  • 47
  • Ok, to simplify to the lowest point I can imagine. Universe inflated to the size of about a solar system at the end of inflationary period, somewhere at 10 -32 seconds. Was it more of a disk or a ball shape then, or something else? – Ska Jan 08 '14 at 22:45
  • 1
    Something else: Roughly resembling the 3-dimensional surface of 4-dimensional sphere, but not quite symmetrical. The precise shape is not exactly known, but probably not too much distorted, like a torus, a cube or a dodecahedron. This is still under investigation; more precise results are expected within a few years, when polarization of the CMB will be analysed. – Gerald Jan 08 '14 at 23:37
  • "Neither the circles-in-the-sky search nor the likelihood method find evidence for a multiply-connected topology" of the Planck paper, section 6.1 means it's not a torus-like or more complex object with holes. – Gerald Jan 08 '14 at 23:49
  • Explanation of simply-connected spaces: http://en.wikipedia.org/wiki/Simply_connected_space. – Gerald Jan 09 '14 at 00:41
  • "A 3-sphere can be constructed topologically by "gluing" together the boundaries of a pair of 3-balls. The boundary of a 3-ball is a 2-sphere, and these two 2-spheres are to be identified. That is, imagine a pair of 3-balls of the same size, then superpose them so that their 2-spherical boundaries match, and let matching pairs of points on the pair of 2-spheres be identically equivalent to each other. In analogy with the case of the 2-sphere (see below), the gluing surface is called an equatorial sphere.", see http://en.wikipedia.org/wiki/3-sphere – Gerald Jan 09 '14 at 00:43
  • Take a 2d-hyperboloid (http://en.wikipedia.org/wiki/Hyperboloid), intersect it with a horizontal plane: you get a circle (1-sphere). Now try to imagine the same with two more dimensions: Adding one dimension returns the surface (2-sphere) of a usual ball in 3d. The next dimension returns a 3-sphere, roughly the shape of a the universe at a fixed cosmic time (http://en.wikipedia.org/wiki/Cosmic_time). – Gerald Jan 09 '14 at 00:55
  • The answer in your first comment is the most precise I heard so far. Now I would like to dig even more :) I understand how 3-sphere "works", but not how it would look like as that "gluing" would lead to some heavy distortions of the "outer" sphere, which would heavily distort the objects inside (imagine a fish in connected spherical containers), but I do get the idea. Is this then 4D geometrical shape? – Ska Jan 10 '14 at 14:05
  • The snapshot is a non-Euclidean surface of a 4D geometrical shape. The gluing leads to distortions, if you try to do it in our everyday's 3D space. It's different in 4D. It can be symmetric there without ugly distortions. – Gerald Jan 10 '14 at 22:22
  • It's the analogon to gluing two discs (2-balls) at the outer circle (1-spheres) to get a 2-sphere (surface of a 3-ball), just one dimension higher. The 2-sphere is ugly in 2D, but nice in 3D. – Gerald Jan 10 '14 at 22:35
  • If you have a few more hours of sparetime, I can recommend the youtube lecture about 4D: http://www.dimensions-math.org/ In English it's staring here: http://www.dimensions-math.org/Dim_reg_E.htm – Gerald Jan 11 '14 at 00:47
  • 1
    ...should have started; the American version still works for me: http://www.youtube.com/embed/6cpTEPT5i0A?list=PL3C690048E1531DC7 – Gerald Jan 11 '14 at 01:01