Is spacetime hyperbolic?

Question

I have always seen answers to this point to measurements of how "flat" local geometry is, but my problem is, thats space not spacetime. I would say its safe to say that the geometry of space in our universe is indeed euclidean, but space isn't over time. The further I look, space should be less, the farther I go, space should be more. To me this seems as if spacetime is hyperbolic along the temporal axis, and that every "instance" cross-section is euclidean. So that ultimately is the question, is spacetime hyperbolic?

Answer 1

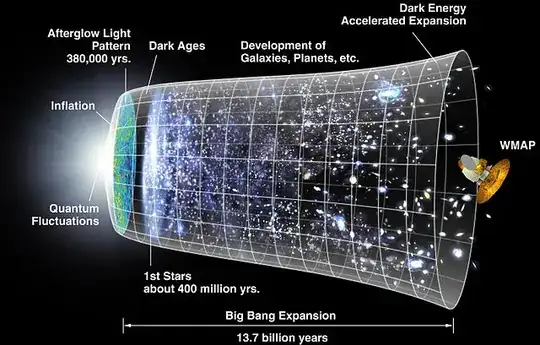
There are three kinds of different hyperbolic in this question and the previous answer by AtmosphericPrisonEscape: the behavior of Lorentz transformations, the spatial hypersurfaces in cosmology (which seem to be flat), and the hyperbolic appearance of spacetime when tracing world lines in a universe with accelerated expansion.

TL;DR: Spacetime is expanding exponentially and if you choose an unconventional hypersurface, that hypersurface is hyperbolic.

Lorentz transformations: Lorentz covariance is the mathematical expression of Einstein's principle of the constancy of the speed of light. Changing the frame of reference of an observer is done by a Lorentz transformation which preserves the light cone and is closely related to the concept of causality. The answer to this question explains this for the Minkowski space, where a Lorentz transform is a hyperbolic rotation.

In this flat (Minkowskian) spacetime:

$$ ds^2 = c\, dt^2 - dx^2 $$

you can use a Lorentz transform to switch to different coordinates $dt$ and $dx$ while the line element $ds$ is invariant, analogous to the hyperbola

$$ 1 = a^2 - b^2. $$

This kind of hyperbolic is not the point of the question.

Cosmology: If we assume large scale homogeneity and isotropy (Copernican principle), we can choose isochronous coordinates. There you have a synchronous time $t$ and spatial hypersurfaces for given $t$ ("time slices"). Freely falling observers are comoving, i.e. have fixed spatial coordinates $\mathbf x$. Their world lines are perpendicular to the spatial hypersurfaces and their proper time matches the synchronous time $\tau = t$. Galaxy clusters are such freely falling observers.

If you take these assumptions and allow time dependence of spatial coordinates on time, you end up with the FLRW metric:

$$ ds^2 = c\, dt^2 - a(t)^2 d\Sigma^2$$

where $d\Sigma^2$ describes the spatial hypersurface. Now additionally to this being a hyperbolic equation, the hypersurfaces $d\Sigma^2$ can have curvature, especially constant positive (closed sphere), zero (Euclidean), or constant negative (open hyperboloid) curvature.

A flat universe is, for example, given by

$$ d\Sigma^2 = dr^2 + r^2 d\Omega,\\ \text{where}\quad d\Omega = d\theta^2 + \sin(\theta)^2\, d\phi^2, $$

which is the metric of Euclidean 3-space in spherical coordinates. Here the only relative acceleration between freely falling observers comes from the scale factor $a(t)$.

A hyperbolic spacetime could be

$$ d\Sigma^2 = dr^2 + \sinh(r)^2 d\Omega $$

which is a hyperbolic plane in spherical coordinates. In such a spacetime, freely falling observers do not only measure a relative acceleration due to the scale factor, but an additional contribution due to the curvature of space.

Expansion: In the FLRW metric you see the scale factor $a(t)$. The Friedmann equations describe the evolution of the scale factor. It does not influence the qualitative shape of the spatial hypersurfaces, but in an expanding space their curvature becomes more and more flat (just like the surface of a sphere locally becomes more and more flat as the sphere expands).

A flat $d\Sigma$ and a constant $a$ gives you no acceleration between freely falling observers whatsoever. An $a$ with constant change manifests as all observers flying apart, but no relative acceleration. Finally, an $a$ with constant acceleration makes everything fly apart ever faster (currently observed). The Friedmann equations tell us, that the behaviour of $a$ changed during the lifetime of the universe as different effects where dominating (radiation, matter, cosmological constant).

Currently we observe an accelerating universe, so $a$ is exponentially increasing (just at the right end of the illustration). If you look at the world line of two Galaxies, their physical distance increases exponentially. Therefore the circumference of a chunk of space increases exponentially, so the hypersurface spanned by a line of freely falling observers is actually hyperbolic (white grid in the illustration). However, I struggle to put that into an equation that clearly shows the hyperbolicity, so don't trust that too much, yet.

Answer 2

As OP still didn't react to the posted answers, I'll try my shot at this.

First of all, I'm not sure what you mean by hyperbolic. A simple Hyperbola $f(x,y) \in R^2$ can be defined by a relation

$$x^2 - y^2 = a^2$$ with some constant $a^2$. One can plot this.

Now the simple Minkowski spacetime metrics from special relativity states that there is a quantity $ds^2$ which stays invariant if an object is observed from different points in spacetime. This invariant quantity can be locally computed from
$$ ds^2 = c^2 dt^2 - dx^2$$ which is a hyperbolic relation and also results from general relativity (the more general variant of special relativity) if one imposes a flat universe.

Now Planck-observations show our universe to be approximately flat, expect for the ripples here and there. By ripples I mean sources of gravity, near which the relation between $dt$ and $dx$ becomes more complicated, and in particular non-hyperbolic.

So if you want to make any statement about 'spacetime', you can only do that about the 'spacetime of our current idea of the universe on a global scale'.