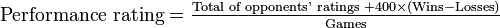What does mathematics have to do with programming?

Question

I just started a diploma in software development. Right now we're starting out with basic Java and such (so right from the bottom you might say) - which is fine, I have no programming experience apart from knowing how to do "Hello World" in Java.

I keep hearing that mathematics is pertinent to coding, but how is it so? What general examples would show how mathematics and programming go together, or are reliant on one another?

I apologize of my question is vague, I'm barely starting to get a rough idea of the kind of world I'm stepping into as a code monkey student...

Answer 1

First off: I am a mathematician - a professional one (in that I get paid for doing maths). I am not a programmer. I do do some programming, but very definitely of the Cargo Cult variety (see first comment to https://tex.stackexchange.com/q/451/86 and my response) and nothing of the sort that would normally bring me to this site (indeed, I registered here to post this answer after seeing a link to it in the TeX chat room).

The summary of my answer is: Mathematics is Programming.

I recently got to teach a mathematics course to a non-mathematical group of students. They were the programming section. I thought this was fantastic! At last, I was going to be able to teach mathematics to people who already understood the basic ideas and who already had a rudimentary toolkit for doing maths. I was incredibly disappointed when I asked how many of them had actually written a program and got an answer somewhere between 0 and 1.

Before I go on, I should clarify a few things. There are areas of mathematics that concern themselves directly with programming and are to do with evaluating algorithms and classifying languages and such-like. I'm not talking about those. There is also a program which is trying to translate all of mathematics into a formal language that can be evaluated by a computer. This is a bit closer to what I'm talking about, but even so to focus on that would miss the main part of what I'm trying to say. The mathematics that I do and the programming that I do are almost completely unrelated by topic. The connection between them is on a different level.

Where I'd like to start is with the comment on the main question:

If that is doing math, then all human activity is a form of math. If that's the case then the word math doesn't have a useful meaning, because it can't be used to distinguish one activity from another.

Yes, that is doing maths. But "maths" is still a useful word because, as the song says, "It ain't what you do, it's the way that you do it.". I would say that I am doing maths when I am approaching something in a mathematical way. Sometimes, that is "hard core" mathematics: formulating definitions, proving theorems. Sometimes, it isn't. Sometimes, it's writing silly little programs so that my kids can learn their spelling words.

This is what mathematics helps me with when I program:

1. Abstraction This is probably the most important transferable skill from mathematics. By this, I mean the ability to strip away all the unnecessary stuff and focus on the important properties.

2. Perspective If I could only choose one thing that all my students were to learn, this would be it: The ability to change ones point of view to suit the problem. We commonly treat this in linear algebra with change-of-basis formulae (that lead to horrendous matrices and horrendous complications), but it is much more applicable than that. At heart, it is the idea that just because something has been presented to you in one fashion, that doesn't have to be the way you work with it. This separates ones view of the thing itself from the way it has been presented. This can be extremely practical: it is all about making something useful or efficient. If I have a list of vectors and it is more efficient to store them as a list of x-coordinates and a list of y-coordinates, so be it.

3. Form versus Function Leading on from the above; if a thing can be presented in many different ways then it is no longer fair to say that one particular presentation is the thing. To misquote that song again: "It ain't what you are it's what you do" that matters.

I could go on, but those are the ones that spring to mind.

Now, there are probably lots of (negative) reactions to what I've written so far. One will be "That's not maths, that's just good sense." (or bad sense) to which I refer to my remark above agreeing with the sentiment that "all human activity is a form of math". Another will be "That isn't the type of maths meant in the question.". This is almost certainly true and here I actually have a lot more sympathy with the person who said "At least I haven't touched the maths for 10 years,". He or she is wrong, of course, they have been doing maths for 10 years because whenever they wrote a program they were doing maths. They just didn't realise it. And here we get to the point about why I was delighted with the (sadly unrealised) possibility of teaching mathematics to students who were already programmers.

I do actually use some "real maths" in my programs. I recently coded a fun 3D shape explorer which involved using some maths to figure out the projections and other transformations that I had to apply to my data. I was mildly amused to find myself actually coding quaternions! But of course, the maths that was involved was trivial compared to the maths that I do when I'm working. It was "back of envelope" stuff. That type of maths, then I agree with the sentiment that you pick it up when you need it, and if you need something more complicated than you can find on Wikipedia then you find a real mathematician to do it for you. However, in order that you can pick it up when you need it then you need to have learnt something. That thing might not be anything you ever actually use, but having learnt that something makes it all the easier to pick up what you do actually use later in life. So this is where I disagree with Coder: you do need to learn some mathematics if you are ever going to use any mathematics and you need to learn it from the mathematical side (which doesn't mean proving theorems, by the way).

And so finally to the "Mathematics is Programming". You can learn all of these things from being a good programmer. And if you've learnt these things, you will find mathematics much easier because you will understand that when we talk about a vector in a vector space then it's just an instance of the class Vector which means that we can do all the things that Vector does to that instance: add, subtract, scale, and so forth. That's why I would love to teach mathematics to programmers. But, speaking as a mathematician, I would say that the first of these, "Abstraction", is easier to learn in mathematics than in programming because mathematics is the pursuit of abstraction. Whenever we see some behaviour our training is always to ask "What is it about that thing that makes it behave in that way? What if I took another thing that was similar, would it behave in the same way? How much of what that thing is would I have to lose for it to stop behaving like that?" (Taking this to the extreme leads to "centipede mathematics" - search for the term). But we don't do this with (just) "real world" objects (whatever they are), we do this with things that have already been abstracted.

This has gone on long enough, so let me close with one of the classic mathematician jokes:

A mathematician and a physicist both attended a seminar on some new model involving 24 dimensional space. Afterwards, they were discussing it and the physicist remarked: "That was really hard. I mean, how does one visualise 24-dimensional space?" to which the mathematician replied: "Oh, it's easy. Just visualise n-dimensional space and then set n = 24.".

---

Added 2012-03-2

There were quite a few comments on this answer expressing a variety of views. These have now been deleted by a moderator on the understanding that I would try to take into incorporate them (or respond to them) in my answer.

However, I'm not sure that I can. Reading those comments and the rest of what's on this page, I can only come to the conclusion that there is a huge misunderstanding as to what mathematics actually is. Moreover, I don't feel competent enough to explain it. Fortunately, someone has already linked to Lockhart's Lament so I'll defer the explanation to that. Whilst I might have put it differently (as I grew up in a scientific environment, I would have put more emphasis on the experimental nature of mathematics), I don't think I could put it better.

I do still think I can add something. As well as the misunderstandings as to what mathematics is, there are also misunderstandings as to what "doing mathematics" means. I see two almost contradictory stances:

1. Mathematics is about equations and formulas. So there's no need to study it because Wikipedia exists (this is almost the converse of Euler's apocryphal challenge to Diderot).

2. Mathematics is about theorems and definitions. So there's no need to study it as programs never prove anything (which is about as complete a fallacy as ... insert favourite fallacy here).

Whilst the two stances contradict each other, they end up in the same place: there's no point in a programmer learning any mathematics - and most assuredly not from a mathematician! After all, what do they know about anything? Anything that a programmer really needs to know can be found in Wikipedia, or cribbed off someone else.

Above, I described myself as a Cargo Cult Programmer. I bet most of you had a private giggle to yourself and thought, "Ah yes, I bet I know what your programs look like then.". You probably felt a bit smug and superior (though I'm sure you felt bad about feeling smug and superior).

What I've described just above is Cargo Cult Mathematics.

So when I say that you should learn a bit of mathematics to understand how mathematics works, I'm saying it for exactly the same reason as you might if you saw a bit of code that I'd written: "How much easier your life would be if you'd stop cut-and-pasting code from StackOverflow and learnt just a bit about how to do it properly.".

The most important thing, though, is that you should learn it from mathematicians. Why so? Here's an analogy. The language that I'm most adept at is TeX. (Says it all, really!). Now, suppose I want to learn a bit more about TeX and it just so happens that Don Knuth is in town and has offered to give some tutorials on TeX. Or I could just read about it on Wikipedia. Or maybe it's Perl and Larry Wall, or C# (is that the right one?) and Jon Skeet. It may well be that these people are not the best teachers, but they sure make up for it in the amount that they know!

And that's what mathematicians are. We're the people who write the actual language, who then write the libraries that you use. Of course, you don't have to know how to prove a theorem - you're not going to write a library! But if you know a bit about how we think, then it might help you understand why we wrote the library the way we did, and if you understand that it might help you make better use of it.

There is a middle ground between looking up equations on Wikipedia and proving the Poincaré conjecture, just as - to refer to Lockhart's lament - there is a middle ground between "I don't really know much about art, but I know what I like" and being Monet, and between "Where's the 'ANY' key?" and being Don Knuth. If you are still in university then you have an amazing opportunity to learn from people who are experts in their area and who - for some reason - are willing to spend their time explaining it to you.

---

The other point I wanted to expand on a bit was why as a programmer you should not be scared of learning a bit more mathematics. It's not the Deep Connections, nor the usefulness. It's that your ability to program a computer can directly help you learn mathematics. I just want to mention a few.

1. Understanding variables. So many people get confused by simple statements like "Let n be a natural number ...". Or "Let epsilon > 0". There are places in mathematics where it's important to remember the scope of a variable. These are all commonplace in programming. Learn to translate a mathematical statement into a program and you'll find it much easier to keep track of what's what.

2. The nature of proof. If you've ever written a test, or written a program to be used by someone else, then you understand the core of proofs. When you do that, you have to know that whatever the user puts in, you can deal with it (insert obligatory xkcd reference here). That's all a proof is! A demonstration that whatever the "user/universe" puts in, the statement will hold. Experimentalists will lean to the "If it works under normal circumstances, it's true" but programmers know that there is always that kid who will try Alt+G+Shift+ÅØÆ just to see what happens.

3. DRY. Sorry to break this to you, but we invented it, not you. We've been "not repeating ourselves" for millennia. That's why I have a copy of Euclid's elements on my shelves and it's still useful.

And there's more. If I knew a bit more about programming, I'd write a book called "Mathematics for Programmers" where the aim wasn't to teach "The mathematics that programmers should know" but "mathematics that everyone should know, but optimised for programmers". But I'll probably never know enough about programming to write it - unless someone offers to collaborate with me!

---

I'll leave it there. Probably if I thought more, I'd change what I've written; hopefully I'd explain it better. In a months' time I might even disagree with parts of it. If anyone wishes to argue further, or comment otherwise, probably best not to do so in the comments here. You know where to find me.

Answer 2

They're not that closely related. For programming, it is important to know about mathematics- especially those branches pertaining to, for example, algorithm performance, but the simple fact is that there is no branch of mathematics that will tell you that Singletons are a horrifically bad idea, for example, or when to favour inheritance over composition, or whether or not you're really going to need that flexibility, and not to repeat yourself, and dozens of other core programming necessities.

Mathematics might be able to express what your program does, but it most certainly cannot tell you the most maintainable, human-readable, feasible way to go about it.

Answer 3

Math and programming are related in two ways.

One is that math can be used to reason about computer programs. It can help answer questions like "How will the running time of my program change as the input data changes?", "Is my program guaranteed to find an answer to my problem?", "Is my program as efficient as it could be?", "How should I re-arrange my program to make it faster or use less memory?". You typically cover topics like these in upper division courses on the theory of computation, the design of algorithms, and computer language design.

The second way math and program are related is that programming is used to solve mathematical problems. This is important because many problems of "ordinary life" can actually be recast as mathematical problems and then solved (maybe approximately) on a computer. These sorts of topics will show up to some extent in almost all of your courses, but particularly in courses on discrete math and mathematical modeling.

Answer 4

Two specific examples where a math education is important to computer science are:

1) Relational databases where relational calculus is used.

Relational calculus consists of two calculi, the tuple relational calculus and the domain relational calculus, that are part of the relational model for databases and provide a declarative way to specify database queries. This in contrast to the relational algebra which is also part of the relational model but provides a more procedural way for specifying queries.

The relational algebra might suggest these steps to retrieve the phone numbers and names of book stores that supply Some Sample Book:

Join book stores and titles over the BookstoreID.
Restrict the result of that join to tuples for the book Some Sample Book.
Project the result of that restriction over StoreName and StorePhone.

The relational calculus would formulate a descriptive, declarative way:

Get StoreName and StorePhone for supplies such that there exists a title BK with the same BookstoreID value and with a BookTitle value of

Some Sample Book.

The relational algebra and the relational calculus are essentially logically equivalent: for any algebraic expression, there is an equivalent expression in the calculus, and vice versa. This result is known as Codd's theorem.

The next area is artificial intelligence (AI) and machine learning.

For an example on how these are used take a look at udacity's class CS 373: PROGRAMMING A ROBOTIC CAR.

Description: This class, taught by one of the foremost experts in AI, will teach you basic methods in Artificial Intelligence, including: probabilistic inference, computer vision, machine learning, and planning, all with a focus on robotics. Extensive programming examples and assignments will apply these methods in the context of building self-driving cars. You will get a chance to visit, via video, the leading research labs in the field, and meet the scientists and engineers who are building self-driving cars at Stanford and Google.

Prerequisites: The instructor will assume solid knowledge of programming, all programming will be in Python. Knowledge of probability and linear algebra will be helpful.

WEEK 1:

Basics of probability Car localization with particle filters

WEEK 2:

Gaussians and continuous probability Tracking other cars with Kalman filters

WEEK 3:

Image Processing and Machine Learning Finding objects in sensor data

WEEK 4:

Planning and search Determining where to drive with A* search Finding optimal routes with dynamic programming

WEEK 5:

Controls Controlling steering and speeds with PID

WEEK 6:

Putting it all together Programming a self-driving car

WEEK 7:

Final Exam Exam testing your knowledge

Answer 5

For scientific application development, Game programming, real-time systems, simulation systems, and such applications, Mathematics is required indeed. After all, programming uses mathematics and science to solve problems. On the other hand, to program an application that captures users information for registering them in your database, does not require any high level of mathematics. Nevertheless, all programmers would benefit from Basic Number Theory, Algebra, Basic Set Theory and Elementary Numerical Analysis.

From the mathematics practitioner side, different topics in Mathematics (as well as many other science branches) could benefit significantly from programming.

Answer 6

I think more than anything else, it's the similarity of the thought process used that makes the two seem so similar.

For example, both are extremely logical. If you follow the same set of steps or same formula, you'll always come up with the same result. For example, 1+1 will always be equal to 2, and set a = 1 means a will always be 1 (until you set it to something else)

Another example is the need to think spatially. In mathematics, I found I often had to hold numbers in my head and visualize what I was doing. As a very simple example, I would break down math problems so that something like 13x13 becomes 13x10 + 13x3, which is much easier for my brain to work with, and I need to keep track that 13x10=130 + 13x3=39, so 130+39 = 169. This same ability to visualize something not visible, or break down a problem into smaller problems is often applied to programming.

So I feel that although you do not need to have a mathematical background to program, where math is defined as performing calculations with numbers, you do need to have similar thought process and understanding as what you would use when solving math problems.

Answer 7

I suppose, to date, you've been taught elements of calculus and some trigonometry. And you call that Mathematics. That's like calling a pair of legs "a human being."

Calculus have little to do with programming, and is more tightly related to physics and engineering. You will need physics for game engines and calculus for statistical analysis. (Statistical analysis drives more jobs that it is comfortable to admit)

Calculus, for us, is more about relating programming to the real world. Computational calculus is the branch that studies how bad that relation is going so far. (spoiler: it's going pretty bad, but we can keep it in check indefinitely)

Trigonometry is a crazy jack in the box that comes out when you least expect it and then signal analysis, audio generation and many other stuff depend on it.

Go trough Algebra 101 and Logic 101, study the history of Pascal, Leibniz, (yeah he almost invented calculus, got it halfway wrong, argued with Newton until it all started making almost sense - and still conceived the binary coding thing) and Babbage and many of your doubts will wane. (your definition of Mathematics will be forever changed, though)

Answer 8

Programming crosses a lot of traditional academic disciplines.

Mathematics, especially applied mathematics, is important to programming because a lot of what we ask computers to do is crunch numbers. Understanding numerical methods and how to apply computation efficiently and appropriately is one of the things many programmers do on a daily basis.

Answer 9

Here I will tell you practical stuff where I have encountered Mathematics in solving some Computing Problems (particularly in Internet domain) :

1. Search Engines uses Vector Calculus for searching data.
2. Matrix Factorization can be used for a lot of stuff like Sentiment Analysis.
3. You need to know Calculus, Summations for figuring out complexity of code that you write.
4. Probability is heavily used in Probabilistic Information Retrieval/Search
5. Naive Bayes Theorem is used in Predictive Analytics.
6. You need to know stuff like hyper plane etc for a concept called SVM which is again used in Machine Learning for solving categorization problems.
7. You need to understand Entropy for doing Natural Language Processing stuff.
8. Latent Semantic Indexing/ Principal Component Analysis used by Search Engines relies heavily on matrix algebra. & so on......

Answer 10

A problem with your question is that "mathematics" and "programming" are both very wide and deep subjects about which there is more to know than anyone could master in a lifetime (no exaggeration). I personally hold an MA degree in mathematics. During my time in university, it seemed as if the more I learned, the less I knew compared to my peers; it felt is if I became less intelligent over the years. When I presented my master's thesis to a group of professors, even most of them seemed to be largely unfamiliar with what I studied.

Likewise, I am now a database-driven web application developer. If you compared me to someone who does embedded assembler language programming, you might think of us as two very talented professionals, but we would have vastly different expertise even though we're both "programmers".

As you progress in your study of higher mathematics (beyond freshman calculus), you will find that mathematics instills a discipline for abstract reasoning that will serve you well when you program. I think that this discipline is very important because you will deal with abstract concerns as you program.

Sure, in freshman programming, you will likely learn about pointer arithmetic. You will write short programs to illustrate this concept and your understanding of how it drives your computer obey your will. However, learning about how pointer arithmetic works in the abstract will not make you good at using pointers in a real program. When it comes time to take on a mess of 10K lines of code and make some changes to the pointer arithmetic, you will need to be able to reason at a very abstract level, making strategic decisions to balance different concerns about how your changes will affect the code.

As a programmer, you must balance "readability" of your code, performance of your code, ease-of-use of the resulting programs, among many other concerns. You must be able to make very abstract comparisons to balance these concerns among one another. You will make many of these comparisons every day. I haven't even gotten started about time-management. You will abstractly reason about the probability that something you do will affect your ability to do your tasks on time, and once again, you will make many decisions every day that will affect your work.

Finally, you must maintain your philosophical discipline to be able to assimilate new ideas and concepts in order to be able to continue on as old methodologies and practices fall out of use. Once again, you will have to be able to evaluate the ideas that come along and make an abstract comparison to what you already know.

In short, programming, as most of us know it, doesn't have a whole lot to do with mathematics, as most of us know it; but when you look at it at an abstract level, they have a lot in common.

Answer 11

Math describes (say) a cubic equation.

An algorithm describes how to solve that cubic equation.

Constructing that (or any) algorithm in a way that can be executed by a machine is programming.

Computer science is the analysis of the algorithm - its theoretical time/space efficiency, error bounds, etc. This much could be considered a branch of mathematics. Note however that computer science and programming are not actually the same thing. It is important to have a foundation in computer science if you want to be a good programmer, because it helps you to better design and reason about the algorithms you develop. But it is not a requirement.

A good programmer may not be (in fact, often is not) a good mathematician, and vice versa. They are separate identifiable skills.

Answer 12

I've seen a lot of questions on thes types of forums through the years where the real problem lay in the poster's poor mathematical understanding. For instance, anyone who has a good foundation in algebra understands that you can't divide by zero. But I've seen many a question where the poster didn't understnd that and subsequently didn't understand the error message that said basically "you can't divide by zero." I've seen a lot of questions where it was clear the poster didn't understand basic logic. I've seen way too many questions where the concepts of boolean algebra where clearly not understood.

Just because you aren't writing mathmatical proofs or directly solving equations like in the math textbook doesn't mean you don't need to understand the concepts behind them. Incidentally, in many years of work experience, I have never run into a bad programmer who had a solid understanding of math.

In some fields you use a lot of mathematics directly, such as game programming, statistical programming, financial programming, some embedded systems. In some of these instances you are given the equations you need in the requirements and sometimes you are not. However even when you are given the equation, translating those equations properly into programming code requires that you understand the equation to begin with.

While you can get by with little more than basic algebra in your basic CRUD application, most of the more interesting problems and more advanced work involves mathematical understanding. So why would you want to limit yourself from the start by not learning mathematics in depth?

Answer 13

Two examples that immediately come to mind are:

functions - The idea of applying a transformation to input variables to produce an output variable is strongly rooted in mathematics. The notion of passing a function around as a parameter to another function even more so. In general, the notion of abstract thinking associated with programing parallels mathematics quite closely.

bitMasks - This common programming approach to solving problems requires at least a basic understanding of boolean algebra to even grasp the concept.

Answer 14

From a programmers perspective: Mathematics is a subset of programming.

Maths applied in programming:

When working with collections (arrays, lists, maps, etc) in programming, then you are dealing with real world implementations of mathematical abstractions.

Programming without maths:

If you do println("Hello World"), then the fact that some math is used to calculate the position on the screen, the length of the string, etc, is really mostly irrelevant.

Using programming for maths:

Implementing mathematics and physics in a programming language makes things like computer aided design possible.

Answer 15

Programming is usually based upon a Model which usually is mathematical model.

Lets take an example of creating a Mortgage Calculator. For this you need to know what interest are, what a compound interst is and so on. If you do not have the understanding of the underlying math then someone else has to provide that information to you. Usually it is the programmer job to do everything. You can always seek help though, if needed.

There are simple concept in mathematics that are used widely in programming. For example expressions, equation, variable, they are profoundly used in programming. If you dont get it in Math, you might not be the best programmer.

Having strong mathematics, give you more stuff to model you your work on. That ultimately makes you a better programmer. For example you may want to draw a quadratic equation in one of your project, this way you learn more stuff just because you are strong in math. Or you write a program to find the area of a circle, give you more experience.

In my short teaching career, I found that if students did not have a math background, they are almost lost when doing a financial problem. If they are lost about the model, learning the language itself become more difficult and honestly very frustrating.

Answer 16

The theoretical foundation of Computer Science (which is more than just programming) is mathematical in nature. Everything from the very definition of computability to the analysis and expression of algorithms to the specifications of programming languages are all based in a wide variety of mathematics. See this Wikipedia page for a flavor of the kind of math involved.

Most of which is not really necessary to know if all you want to do is sling code. As far as applied math goes, unless you go into a field that requires serious number-crunching skills (detailed physical simulations, signal analysis, financial analysis and prediction, etc.) you're probably not going to use anything more involved than basic algebra on a day-to-day basis.

Answer 17

It honestly depends on what sort of programming you're doing.

If you're making light web apps with some logic, you probably don't need the more advanced math classes that many degrees require. If you're working with things that are a bit more processor heavy, than you're going to need more math. If you're doing work with any kind of scientific field, you'll really want to keep your calc references at hand.

Another place where you'll need math is if you want to write games. The second you want to move diagonally, you'll need to start doing some careful calculations so that you don't end up with characters that accelerate if the move to a block to the NE.

That said, you don't necessarily need to learn math, then learn programming. It's perfectly valid to learn programming, then pick up some advanced math. I started coding before I ever set foot inside a Calc or Trig class and did just fine. When I did start learning advanced math, I found that coding really helped me, as I could explore the topic more by changing variables in a quick script than I could with pen and paper.

Answer 18

I'm by no means an expert at math! I did well in HS Geometry, which was all logic to me. I find programming and geometry to be very similar. Boolean logic ties very well in my mind to geometric proofs.

Then there's little things like knowing that you can control how many columns are in a row using the modulus operator.

I strongly favor the idea of being a good programmer who has a friend (or colleague / consultant) who is a good mathematician.

Obviously if you're blessed to have both skillsets, run with it!

Answer 19

Simple answer; Math makes you fast. Sure, you can google/se/wikipedia your coding problems away, but get enough math done and you won't need to. Believe it or not, the properly trained human brain is faster than google. Moreover the more math you know the faster you will be able to understand the results google/se/wiki gives you, and the less you'll need to drill down to understand what people tell you. In the process of solving your programming problems you'll end up learning math anyway but if you focus on math it will be a far more efficient process.

Your question is kind of like a rock musician asking why they would need formal musical training. Is it possible to be successful without it? Sure. Does it make you much more of a badass if you do go with it? Absolutely.

Slightly more complicated answer - When mathematicians and programmers use the word "solution" (for problems, that is, not equations - ie not "roots") - they mean pretty much the same thing. Learning to solve math problems helps you to learn to solve programming problems.

BTW - and no offense intended to anybody whatsoever - anybody who says s/he is a good programmer but s/he hates math is a Big Fat Liar. What happened was, they got turned off of formal math by a bad hs or college instructor and ever since then they feel like they "aren't good at math". Anybody without a learning disability (ie anybody capable of learning an OO language) is capable of everything up to and including Sophomore Calculus.

Answer 20

The actions of doing Mathematics and 99% of Programming have very little in common. Math is not required to be a great programmer. I've taken several college level courses in math, including but not limited to Calculus I,II,III elements of linear algebra, and several others.

I've been a software engineer for over 10 years and only rarely needed to use anything more than basic mathematics. There are some exceptions where mathematics is needed: like graphics and other areas. But 99% of the programming and software engineering doesn't require Math. It requires logical thinking, algorithms, OOP, functions, decomposing problems, etc.

Answer 21

1) As you learn programming, you will come across technical jargon(i.e., algorithm). To analyse algorithm, one has to have an idea about the nature of polynomial, logarithmic and exponential functions.

2) Based on a computer science application, one has to have an idea on discrete maths and continuous maths to write meaningful solution. One can understand more on this by going through such courses like-

---> Mathematics for Computer Science

---> Coding the Matrix: Linear Algebra through Computer Science Applications.

For a beginner, I feel dynamic typed languages like python/scheme are the first best languages for programming. Static typed languages like Java/C++ are not the best to start with. Opencourseware published from "MIT/UOC-Berkeley/Stanford" can guide you better than a regular college curriculum. I bet you!!!

Answer 22

I would personally say, it depends upon the level of programming that is involved. The data models and the correlations between those, the programming algorithms involved. For eg: to write a program that outputs "Hello World", i see no requirement for familiarizing someone with Higher Mathematics. The level of Mathematical involvement would depend upon the level of complexity of the problem that needs to be solved programaticaly.

Answer 23

Someone almost hit the nail on the head above. Programming is mathematics. More specifically, programming is a branch of mathematical logic called computability theory or recursion theory.

Other branches of math are involved directly, specifically formal language and automata theory. These help describe regular expressions, used in pattern matching, and formal grammars, used to describe and parse programming languages.

Anybody who says that programming is not mathematics either doesn't know what they're talking about, or has an ulterior motive, like a "Intellectual Property" maximalist, who hopes to profit by getting a patent on an algorithm or some other basic mathematical fact or discovery.

Some references for programming as math, and the corollary not knowing what you're talking about:

Program are Proofs: 19th Century Logic and 21st Century Computing

Programs are Proofs: Models and Types in Lambda Calculus

Wikipedia's Curry-Howard Correspondence article

On the Unusual Effectiveness of Logic in Computer Science

The Unreasonable Effectiveness of Logic

Yes, those are heavy on the "logic" part of mathematical logic, but mathematics is generally acknowledged to be a few axioms, and their logic consequences as developed via first order logic.

As far as saying otherwise and being an "IP" maximalist out for money:

How to patent an algorithm in the US. Algorithms aren't patentable, but patents are granted on algorithms by not referring to them as algorithms. It's not hard to find a lot of material on the web that either points out, or attempts to explain, that contradiction.

Answer 24

Just my experience, no more :
I'm not mathematicien. I'm not a genius, just a autodidact.
... and after many years, I realize than I work with intuition

First I learned Pick (dead system) from scratch (alone with paper documentation and samples),
... after C, C++ for fun, and Java for work.

As you told about it, I can say that learning this language is not a mathematical problem (even if basic/minimalist algebra help you,) but a logical one.

Now many tools (like Eclipse) help and correct you : you have to focus to what you want to do, with only 52 reserved words ... and many libraries which have down work for you.

So if you like language, choose a Java project, study Pattern Design, UML, understand JVM and how use it with Bigloo and Scala, understand again and again during 10 000 hours.

Experience in Java give you well paid jobs, and for a long time in industrial big projects, and you will be able to switch to another environment because you are able to speak informatic, not mathematic.

If understanding language (words, meaning, concept and other hided logical sciences like semantic, ontology, ..) is a good objective for your human person, for all your life, you can begin now.

Otherwise, experiment another way.

Best regards
Claude

Answer 25

Mathematics is everything to do with programming. For example, in game programming you need to use matyhs for the physics and to do more less everything. To move the player's x position in Java you would do int x = x + speed * deltaTime or int x = x - speed * deltaTime But you might say that that is basic maths so lets move onto more advanced stuff. There is an algorithm for rating chess players called the Elo Algorithm.

If you still think that this is basic then try this. How do you calculate someones age when you are given a birth day, month and year. Subtract birth year from this year and then check if month is less than this month and if it isn't subtract 1.

It isn't magic it is hard work and good mathematics.

Answer 26

Ok, I'm probably going to get a ton of down-votes for this, but programming and maths are two completely unrelated things. Someone can be an amazing developer knowing only the basics like addition, multiplication and basic logical operations.

Most of the developers will not solve a single equation during their professional career, and things like big O notation can be grasped in non mathematical way as well. You just think about the stuff, imagine bits flipped in your head, and voila, you can tell what kind of big O the stuff is, if someone explains what log and power is.

Sometimes math can make it simple, or it can make you feel proud that you proved something, since you can extend the meaning of programming to a mathematical domain via naming it discrete maths and such, but learning a lot of differential equations and integrals, and how to prove that, is IMHO not exactly the best idea what to do if you want to succeed as a programmer.

At least I haven't touched the maths for 10 years, I had arguments with my math professors all the time, and when I needed a math for realtime rendering, I learned everything from programmers side of view, without any proving any theorems, and for me it was simple and easy to grasp compared to all the stuff math professors where putting in our heads with a comment of "you can't be a good programmer if you don't know the math". Sure you can, easy!

I now know the mathematical stuff, so that I can talk with math-background programmers with all the log's differentials and stuff, but only for the reason so that they wouldn't faint. Because that stuff is useless 99.9% of the time, and when it is, it can be learned 1000x more effectively from programmers viewpoint.

Heck, programmers need at least 5 years to master a programming language+frameworks+best practices. Why on earth they should learn how to prove the theorems? Math student's do the math stuff, programmers get that stuff running, that's how it should work.