This is the exercise 4.23 from Nielsen and Chuang, asking that if it is possible to construct $C^1(U)$ for $U=R_{x,y}(\theta)$ with TWO single qubit gates and CNOT gate. My answer is no, and I would like to argue in the following way.
First, we do have such a construction for $U=R_z(\theta)$ which is the following (sorry that I have to draw it by hand)
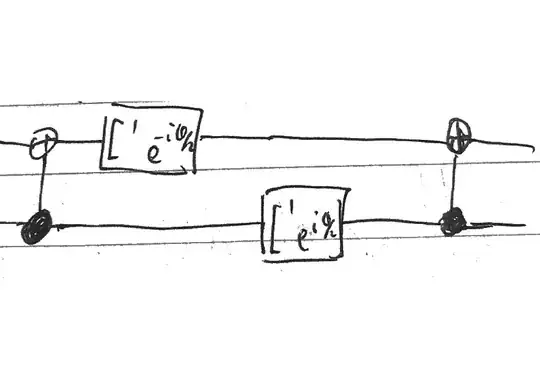
where the (reverse) CNOT has the matrix representation
$$ \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ \end{bmatrix} $$ such that we have the matrix representation of the circuit as $$ \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ \end{bmatrix} \big( \begin{bmatrix} 1 & 0 \\ 0 & e^{-i\theta/2} \end{bmatrix} \otimes \begin{bmatrix} 1 & 0 \\ 0 & e^{i\theta/2} \end{bmatrix} \big) \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & e^{-i\theta/2} & 0 \\ 0 & 0 & 0 & e^{i\theta/2} \\ \end{bmatrix} $$
which is the desired matrix for $C^1(R_z(\theta))$. Thus we do a have a circuit with only two single qubit gates and CNOT for $U=R_z(\theta)$. Now for the rotation $U=R_x(\theta) = VR_z(\theta)V^\dagger$, which differ from $R_z$ by a unitary transformation V, we will need to "sandwich" the above circuit by some other gate. However, that is not possible by just one single qubit gate as we need unitary transformation on both sides of the circuit, despite we may merge two gates into one. Thus I feel that it is not possible for $U=R_{x,y}$. However, on the other hand, physically there is no difference between various rotation operators, it feels not right that only $R_z$ has such circuit construction but not for others. So I may have missed sth here, and any help and clarification is appreciated.
