Measuring in an arbitrary basis

Question

I'm new to quantum computing, so apologize if my question seems obvious.

Say we have a state $|\Psi\rangle$ and we want to measure it in the computational basis. From what I've been able to understand so far is that, when we make a measure in the computational basis, we obtain a classical bit with a certain probability. For instance if: $$|\Psi\rangle\phantom{} = \alpha|0\rangle+\beta|1\rangle$$ then, once we measure, we obtain $0$ with probability $|\alpha|^2$ and obtain $1$ with probability $|\beta|^2$

Where I truly get lost is when I am asked to measure a state in another basis. For instance, let's say that I am asked to measure $|\Psi\rangle$ in the following basis: $$\{|\alpha\rangle, |\alpha_{\bot}\rangle\}$$ where $\alpha = \frac{\pi}{4}$. I am totally lost here, as I don't know what $|\alpha>$ is. It's a vector of 2 components, I guess. Intuitively, I would have said that $|\alpha\rangle = \alpha|0\rangle$, but I am honestly not sure. Even if that is true, I have no idea what $|\alpha_{\bot}\rangle$ would be like. Could you help me out to clarify this, please?

PS: I don't have a background in physics. I have one in Computer Science. I'm discovering quantum computing on my free time

Answer 1

You're happy with the concept of measuring in the computational basis, so stick with that for now. Measuring in another basis simply means applying a unitary before the measurement. Unitaries are basis transformations, meaning they change some basis, say $|\alpha\rangle,|\alpha^\perp\rangle$ into another basis such as $|0\rangle,|1\rangle$. Indeed, we can deliberately construct unitaries in this way: $$ U=|0\rangle\langle\alpha|+|1\rangle\langle\alpha^\perp| $$ For example, if we started with an initial state $|\alpha\rangle$, then applying $U$ converts if to $|0\rangle$ and so when you measure it, you definitely get answer $|0\rangle$, corresponding the the original state having definitely been in the state $|\alpha\rangle$.

As for the notation of what $|\alpha\rangle$ means: remember that the text inside the ket, in this case $\alpha$, is an arbitrary label that doesn't mean anything unless you ascribe a meaning to it. So it's just there to denote "some state", presumably a one-qubit state from this context. So, that implicitly means an arbitrary normalised vector such as $\alpha|0\rangle+\beta|1\rangle$ where $|\alpha|^2+|\beta|^2=1$. It could be a bit confusing to have $\alpha$ appear in both the label and one of the amplitudes but that's why, personally, I wouldn't ever make the label $\alpha$. Now it might be that whatever source you're using has ascribed a particular meaning to the concept $|\alpha\rangle$. Since you're talking about it being an angle, I'm guessing it means $\cos\alpha|0\rangle+\sin\alpha|1\rangle$, but that would be highly source dependent because I could just as easily imagine a source using $\cos\frac{\alpha}{2}|0\rangle+\sin\frac{\alpha}{2}|1\rangle$ or even $(|0\rangle+e^{i\alpha}|1\rangle)/\sqrt{2}$.

On the other hand, the meaning of $|\alpha^\perp\rangle$ is pretty clear: a state that or orthogonal to $|\alpha\rangle$. For a qubit that means it has to be (up to a global phase) $\beta^\star|0\rangle-\alpha^\star|1\rangle$

Answer 2

In simple words, measuring in another basis than computational one means that you express a quantum state $|\psi\rangle$ like a linear combination of two vectors different from $|0\rangle$ and $|1\rangle$.

An example of another basis is x-basis (or Hadamard basis). In this case, base vectors are $|+\rangle = \frac{1}{\sqrt{2}}\begin{pmatrix}1\\1\end{pmatrix}$ and $|-\rangle = \frac{1}{\sqrt{2}}\begin{pmatrix}1\\-1\end{pmatrix}$. To measure in this basis, you firstly have put Hadamard gate $H$ before a measurement in a quantum circuit. Your result will be again vectors $|0\rangle$ and $|1\rangle$ but $|0\rangle$ corresponds to $|+\rangle$ and $|1\rangle$ to $|-\rangle$. As a result, you are able to express $|\psi\rangle$ like a combination of $|+\rangle$ and $|-\rangle$.

Similarly, it is possible to measure in many different basis, however, firstly you have to find a circuit transforming the basis to a computational one and to apply it before measuring.

Answer 3

$\newcommand{\ket}[1]{|#1⟩}$ Let's assume the state $\ket{\Psi}$ is written in an arbitrary basis, say $(\ket{a},\ket{b})$, as:

$\ket{\Psi} = \alpha \ket{a} + \beta \ket{b}$, where $\alpha$ and $\beta$ are complex coefficients

Denoting the eigenvalues of the basis as $A$ and $B$ respectively, according to Born's rule of measurement, there is a probability $|a|^2$ of measuring $A$ and $|b|^2$ of measuring B.

Given a state $\ket{\alpha}$, $\ket{\alpha_{\perp}}$ is its orthogonal state. Writing the states as vectors, the two vectors are orthogonal. It is true that in a Euclidean vector space of dimension $n \geq 3$ (3D space, if you will), a vector has infinitely many orthogonal vectors. In the case of a 1-qubit state, however, we're actually in the $n = 2$ case! In geometric terms, we're in 2D space. This means that we actually have only two vectors that are orthogonal to the vector in question.

To know which one to choose, we have to refer to the Bloch sphere representation of 1-qubit bases.

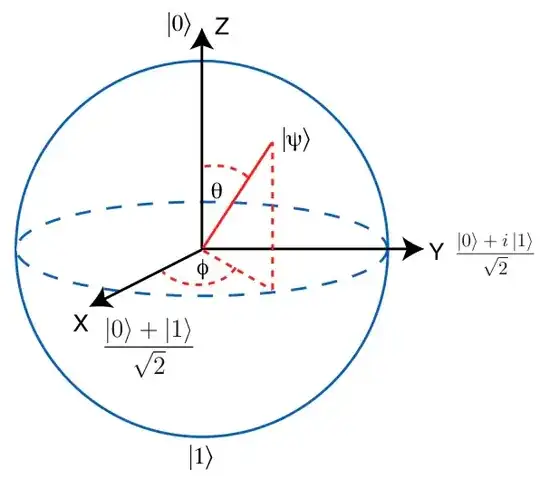
On the Bloch sphere, two orthogonal vectors are colinear. To find an orthogonal vector of another vector in order to form a basis, we just take the vector obtained by central symmetry. For instance, in the above figure, if we take $\ket{\psi}$ defined by the angles $\theta$ and $\phi$ as the vector, the other vector $\ket{\psi_{\perp}}$ will be defined by the angles $\theta + \pi$ and $\phi + \pi$.

Now as to what $\ket{\alpha}$ with $\alpha = \frac{\pi}{4}$, I believe it means a vector with $\theta = \frac{\pi}{4}$, as the $\phi$ angle is just responsible for a phase constant and does not affect measurement. In short, pick any vector with $\theta = \frac{\pi}{4}$, then find its orthogonal vector by central symmetry.

I've only very rarely encountered this notation however and find it very confusing, especially for an introductory text in quantum computing.

The section below is meant to prepare you for the same notation you just encountered in a different context, so as to prevent you from confusing the two.

Usually, quantum circuits have registers of width not bound to 1 qubit. While there is no ambiguity in the case of 1 qubit, the following notations can be used in the case of multi-qubit registers (in order of decreasing explicitness), where we choose the binary representation of the number $5$ as the state of a 3-qubit register.

1. $\ket{1} \otimes \ket{0} \otimes \ket{1}$
2. $\ket{101}_3$, the subscript denoting the width of the register
3. $\ket{5}_3$, where we switch to decimal base
4. $\ket{5}$, where we forego the width of the register

The $5$ which we chose arbitrarily before, can actually be any positive (unsigned) integer representable with 3 qubits.

For 1-qubit numbers, a basis has 2 elements (in the computational basis, $\ket{0}$ and $\ket{1}$). For 2-qubit numbers, the basis has 4 elements (in the computational basis, $\ket{00}$, $\ket{01}$, $\ket{10}$ and $\ket{11}$). For $n$-qubit numbers, the basis has $2^n$ elements.

Notice that the aforementioned bases can also be written with the notation conventions as:

• $\ket{0}$, $\ket{1}$, $\ket{2}$, $\ket{3}$, in the case of $n = 2$
• $\ket{0}$, $\ket{1}$, $\ldots$, $\ket{2^n - 1}$, in the general case