2

Is there a way of eliminating a term of a superposition state? Let's say I have the state

$$\frac{1}{\sqrt 2}|00\rangle + \frac{1}{2}|01\rangle + \frac{1}{2}|10\rangle$$

What operation would I do to eliminate the state $|00\rangle$? And be left with only the terms $|01\rangle + |10\rangle$. I'm looking for a general solution, an idea, rather than one specific to this case.

Sanchayan Dutta
  • 17,497
  • 7
  • 48
  • 110
Sorin Bolos
  • 611
  • 5
  • 11

1 Answers1

1

If you've got

$$|\Psi\rangle = \frac{1}{\sqrt{2}}|00\rangle+\frac{1}{2} \Big( |01\rangle + |10\rangle \Big)$$

and you want to suppress state $|00\rangle$ using two ancillary qubits, you can

  • apply a negated Toffoli gate to an ancillary qubit q[2] as target
  • apply Hadamard to a second ancillary q[3]
  • Toffoli $\mathbf{CCX}(q[2],q[3],q[0])$
  • $\mathbf{X}(q[3])$
  • $\mathbf{CCX}(q[2],q[3],q[1])$

and you'll obtain

$$|\Psi_1\rangle = \frac{1}{\sqrt{2}}\Big( |01\rangle + |10\rangle \Big)$$

Simplyfing:

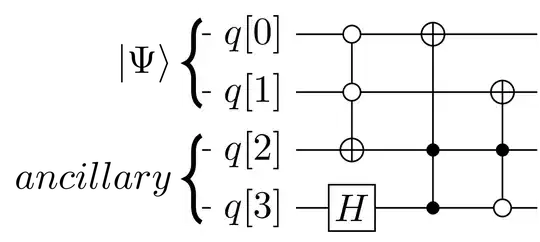
enter image description here

In general (if the state $|\Psi\rangle$ is not a simple superposition) you can use a negated Toffoli gate (or a series of $n-1$ negated Toffoli gates for an input register of $n$ qubits) to get the state $|00\rangle$ (or the state $|0\rangle^n$ for an input register of $n$ qubits) to an ancillary qubit (or $n-1$ ancillary qubits) and then suppress it to obtain the desired result (this depends on the result you want to obtain).

maxdevblock
  • 31
  • 2