That's not the right way to look at it. In quantum mechanics, time evolutions are considered to be unitary and any unitary evolution can be written as a sequence of unitary operators $U_1, U_2, U_3,\ldots$ acting on a quantum state $|\Psi\rangle$. Any single-qubit unitary operation is a $2\times 2$ matrix of the form:
$$U=\begin{pmatrix}a&b\\-e^{i\phi}b^*&e^{i\phi} a^*\end{pmatrix}, |a|^2+|b|^2=1.$$
In your case, $a=\frac{i}{\sqrt{2}}$, $b=\frac{1}{\sqrt{2}}$ and $\phi=\pi$. Now, $B$ isn't one of the "popular" quantum gates like the Pauli or the Hadamard, but that doesn't mean it can't be a valid evolution operator! The Hadamard and the Pauli are generally chosen because they have some neat properties; for instance, the Pauli matrices form a basis for all $2\times 2$ Hermitian matrices. For more, read the Wikipedia pages on Hadamard matrix and Pauli matrices. Moreover, note that some gates can be easier to engineer than others; I had written an answer about this before. Also see: Why do we use the standard gate set that we do?.
So for drawing quantum circuits we generally try to choose a universal gate set that's also relatively easy to physically implement. Now any unitary evolution can be replicated with an $\epsilon>0$ precision, with a sufficient number of elementary quantum gates which form a universal set. Niel de Beaudrap also wrote a nice answer on this topic. Perhaps, as an exercise, you can try to write the $B$ gate in terms of the elementary quantum gates listed here?
If you notice carefully, $\sqrt{\operatorname{NOT}}=\frac{1-i}{\sqrt{2}}B$. That is, $B$ differs from the $\sqrt{\operatorname{NOT}}$ (or $\sqrt{X}$) by a simple phase factor! Thus, $\sqrt{\operatorname{NOT}}$ and $B$ are essentially the same gate cf. Norbert Schuch's answer. For a physical implementation of $\sqrt{\operatorname{NOT}}$ check Jones, Hansen & Mosca (1998).
I suggest playing around with it a bit on Quirk. The Bloch sphere intuition should help:
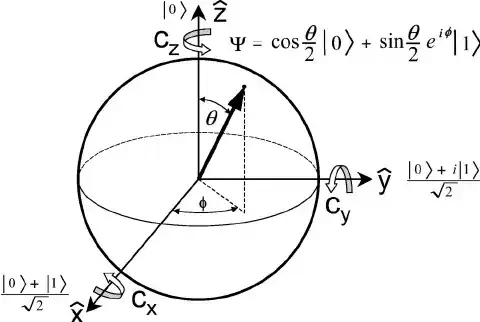
You see, both $\sqrt{X}$ and $B$ rotate a qubit state around $\hat{x}$ by $90^{\mathrm{o}}$, albeit with different phase factors.
