2-Qubit Gate Teleportation with 1 Maximally Entangled State for Distributed Computation

Question

$\newcommand{\ket}[1]{|#1\rangle}$

I search for quantum circuits/protocols that enable distributed quantum computation of a 2-qubit gate using gate teleportation.

Let me explain the desired scenario with an example from here: arXiv:2002.11808 (Fig. 8).

SOURCE and DESTINATION are 2 different parties that share a maximally entangled state ($\ket{\Phi^+}$). Each party has a qubit, $\ket{\psi}$ and $\ket{\phi}$ respectively. The depicted circuit computes $CNOT(\ket{\psi}\otimes\ket{\phi})$ using the maximally entangled state. Note, that this circuit only uses 1 maximally entangled qubit pair and in the end SOURCE and DESTINATION both "keep their qubit".

I aim to generalize this circuit to compute an arbitrary 2-qubit gate or find similar circuits for other 2-qubit gates. Other circuits should also have the 2 properties:

• use only 1 maximally entangled state
• both parties "keep their qubit"

---

My results so far

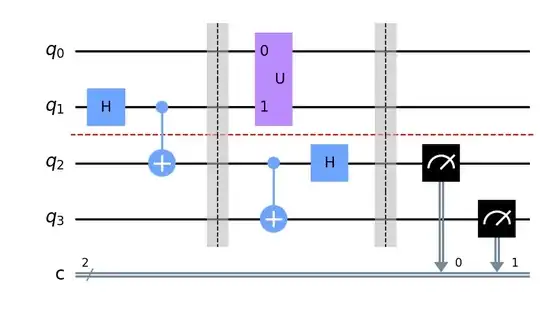
I already tried replacing the CNOT of SOURCE by an arbitrary 2-qubit gate:

(First entangle $q_1$ and $q_2$, then attempted gate teleportation)

But I can't find any compensations (the part after measuring, terminology from this answer) that yield the desired result.

From looking at the resulting state it makes sense (to me) that this circuit doesn't work for arbitrary 2-qubit gates. Assume $U$ is the matrix of a 2-qubit gate, then:

$\displaystyle U(\ket{\psi}\otimes\ket{\phi})=\left[\begin{matrix}\color{red}{u_{0}} & \color{green}{u_{1}} & \color{blue}{u_{2}} & \color{cyan}{u_{3}}\\\color{magenta}{u_{4}} & \color{yellow}{u_{5}} & \color{black}{u_{6}} & \color{gray}{u_{7}}\\\color{brown}{u_{8}} & \color{lime}{u_{9}} & \color{olive}{u_{10}} & \color{orange}{u_{11}}\\\color{pink}{u_{12}} & \color{purple}{u_{13}} & \color{teal}{u_{14}} & \color{violet}{u_{15}}\end{matrix}\right]\cdot\left[\begin{matrix}\psi_{0} \phi_{0}\\\psi_{0} \phi_{1}\\\psi_{1} \phi_{0}\\\psi_{1} \phi_{1}\end{matrix}\right]=\left[\begin{matrix}\psi_{0} \phi_{0} \color{red}{u_{0}} + \psi_{0} \phi_{1} \color{green}{u_{1}} + \psi_{1} \phi_{0} \color{blue}{u_{2}} + \psi_{1} \phi_{1} \color{cyan}{u_{3}}\\\psi_{0} \phi_{0} \color{magenta}{u_{4}} + \psi_{0} \phi_{1} \color{yellow}{u_{5}} + \psi_{1} \phi_{0} \color{black}{u_{6}} + \psi_{1} \phi_{1} \color{gray}{u_{7}}\\\psi_{0} \phi_{0} \color{brown}{u_{8}} + \psi_{0} \phi_{1} \color{lime}{u_{9}} + \psi_{1} \phi_{0} \color{olive}{u_{10}} + \psi_{1} \phi_{1} \color{orange}{u_{11}}\\\psi_{0} \phi_{0} \color{pink}{u_{12}} + \psi_{0} \phi_{1} \color{purple}{u_{13}} + \psi_{1} \phi_{0} \color{teal}{u_{14}} + \psi_{1} \phi_{1} \color{violet}{u_{15}}\end{matrix}\right]$

If I use $U$ in the circuit and measure qubits $q_1$ and $q_2$ we get the following states for $\ket{\psi}\otimes\ket{\phi}$ ($=q_0\otimes q_3$) written as $\ket{q_1q_2}\rightarrow \ket{\psi\phi}$:

$$\displaystyle \ket{00}\rightarrow\left[\begin{matrix}\psi_{0} \phi_{0} \color{red}{u_{0}} + \psi_{0} \phi_{1} \color{green}{u_{1}} + \psi_{1} \phi_{0} \color{blue}{u_{2}} + \psi_{1} \phi_{1} \color{cyan}{u_{3}}\\\psi_{0} \phi_{0} \color{green}{u_{1}} + \psi_{0} \phi_{1} \color{red}{u_{0}} + \psi_{1} \phi_{0} \color{cyan}{u_{3}} + \psi_{1} \phi_{1} \color{blue}{u_{2}}\\\psi_{0} \phi_{0} \color{brown}{u_{8}} + \psi_{0} \phi_{1} \color{lime}{u_{9}} + \psi_{1} \phi_{0} \color{olive}{u_{10}} + \psi_{1} \phi_{1} \color{orange}{u_{11}}\\\psi_{0} \phi_{0} \color{lime}{u_{9}} + \psi_{0} \phi_{1} \color{brown}{u_{8}} + \psi_{1} \phi_{0} \color{orange}{u_{11}} + \psi_{1} \phi_{1} \color{olive}{u_{10}}\end{matrix}\right]$$

$$\displaystyle \ket{01}\rightarrow\left[\begin{matrix}\psi_{0} \phi_{0} \color{red}{u_{0}} - \psi_{0} \phi_{1} \color{green}{u_{1}} + \psi_{1} \phi_{0} \color{blue}{u_{2}} - \psi_{1} \phi_{1} \color{cyan}{u_{3}}\\- \psi_{0} \phi_{0} \color{green}{u_{1}} + \psi_{0} \phi_{1} \color{red}{u_{0}} - \psi_{1} \phi_{0} \color{cyan}{u_{3}} + \psi_{1} \phi_{1} \color{blue}{u_{2}}\\\psi_{0} \phi_{0} \color{brown}{u_{8}} - \psi_{0} \phi_{1} \color{lime}{u_{9}} + \psi_{1} \phi_{0} \color{olive}{u_{10}} - \psi_{1} \phi_{1} \color{orange}{u_{11}}\\- \psi_{0} \phi_{0} \color{lime}{u_{9}} + \psi_{0} \phi_{1} \color{brown}{u_{8}} - \psi_{1} \phi_{0} \color{orange}{u_{11}} + \psi_{1} \phi_{1} \color{olive}{u_{10}}\end{matrix}\right]$$

$$\displaystyle \ket{10}\rightarrow\left[\begin{matrix}\psi_{0} \phi_{0} \color{magenta}{u_{4}} + \psi_{0} \phi_{1} \color{yellow}{u_{5}} + \psi_{1} \phi_{0} \color{black}{u_{6}} + \psi_{1} \phi_{1} \color{gray}{u_{7}}\\\psi_{0} \phi_{0} \color{yellow}{u_{5}} + \psi_{0} \phi_{1} \color{magenta}{u_{4}} + \psi_{1} \phi_{0} \color{gray}{u_{7}} + \psi_{1} \phi_{1} \color{black}{u_{6}}\\\psi_{0} \phi_{0} \color{pink}{u_{12}} + \psi_{0} \phi_{1} \color{purple}{u_{13}} + \psi_{1} \phi_{0} \color{teal}{u_{14}} + \psi_{1} \phi_{1} \color{violet}{u_{15}}\\\psi_{0} \phi_{0} \color{purple}{u_{13}} + \psi_{0} \phi_{1} \color{pink}{u_{12}} + \psi_{1} \phi_{0} \color{violet}{u_{15}} + \psi_{1} \phi_{1} \color{teal}{u_{14}}\end{matrix}\right]$$

$$\displaystyle \ket{11}\rightarrow\left[\begin{matrix}\psi_{0} \phi_{0} \color{magenta}{u_{4}} - \psi_{0} \phi_{1} \color{yellow}{u_{5}} + \psi_{1} \phi_{0} \color{black}{u_{6}} - \psi_{1} \phi_{1} \color{gray}{u_{7}}\\- \psi_{0} \phi_{0} \color{yellow}{u_{5}} + \psi_{0} \phi_{1} \color{magenta}{u_{4}} - \psi_{1} \phi_{0} \color{gray}{u_{7}} + \psi_{1} \phi_{1} \color{black}{u_{6}}\\\psi_{0} \phi_{0} \color{pink}{u_{12}} - \psi_{0} \phi_{1} \color{purple}{u_{13}} + \psi_{1} \phi_{0} \color{teal}{u_{14}} - \psi_{1} \phi_{1} \color{violet}{u_{15}}\\- \psi_{0} \phi_{0} \color{purple}{u_{13}} + \psi_{0} \phi_{1} \color{pink}{u_{12}} - \psi_{1} \phi_{0} \color{violet}{u_{15}} + \psi_{1} \phi_{1} \color{teal}{u_{14}}\end{matrix}\right]$$

Since $\ket{\psi\phi}$ is always missing some $u_x$ I don't see how this circuit could be used to compute arbitrary 2-qubit gates.

---

If I change the circuit to measure qubits $q_2$ and $q_3$:

the state $\ket{q_0q_1}$ contains all $u_x$:

$$\displaystyle \ket{00}\rightarrow\left[\begin{matrix}\psi_{0} \phi_{0} \color{red}{u_{0}} + \psi_{0} \phi_{1} \color{green}{u_{1}} + \psi_{1} \phi_{0} \color{blue}{u_{2}} + \psi_{1} \phi_{1} \color{cyan}{u_{3}}\\\psi_{0} \phi_{0} \color{magenta}{u_{4}} + \psi_{0} \phi_{1} \color{yellow}{u_{5}} + \psi_{1} \phi_{0} \color{black}{u_{6}} + \psi_{1} \phi_{1} \color{gray}{u_{7}}\\\psi_{0} \phi_{0} \color{brown}{u_{8}} + \psi_{0} \phi_{1} \color{lime}{u_{9}} + \psi_{1} \phi_{0} \color{olive}{u_{10}} + \psi_{1} \phi_{1} \color{orange}{u_{11}}\\\psi_{0} \phi_{0} \color{pink}{u_{12}} + \psi_{0} \phi_{1} \color{purple}{u_{13}} + \psi_{1} \phi_{0} \color{teal}{u_{14}} + \psi_{1} \phi_{1} \color{violet}{u_{15}}\end{matrix}\right]$$

$$\displaystyle \ket{01}\rightarrow\left[\begin{matrix}\psi_{0} \phi_{0} \color{green}{u_{1}} + \psi_{0} \phi_{1} \color{red}{u_{0}} + \psi_{1} \phi_{0} \color{cyan}{u_{3}} + \psi_{1} \phi_{1} \color{blue}{u_{2}}\\\psi_{0} \phi_{0} \color{yellow}{u_{5}} + \psi_{0} \phi_{1} \color{magenta}{u_{4}} + \psi_{1} \phi_{0} \color{gray}{u_{7}} + \psi_{1} \phi_{1} \color{black}{u_{6}}\\\psi_{0} \phi_{0} \color{lime}{u_{9}} + \psi_{0} \phi_{1} \color{brown}{u_{8}} + \psi_{1} \phi_{0} \color{orange}{u_{11}} + \psi_{1} \phi_{1} \color{olive}{u_{10}}\\\psi_{0} \phi_{0} \color{purple}{u_{13}} + \psi_{0} \phi_{1} \color{pink}{u_{12}} + \psi_{1} \phi_{0} \color{violet}{u_{15}} + \psi_{1} \phi_{1} \color{teal}{u_{14}}\end{matrix}\right]$$

$$\displaystyle \ket{10}\rightarrow\left[\begin{matrix}\psi_{0} \phi_{0} \color{red}{u_{0}} - \psi_{0} \phi_{1} \color{green}{u_{1}} + \psi_{1} \phi_{0} \color{blue}{u_{2}} - \psi_{1} \phi_{1} \color{cyan}{u_{3}}\\\psi_{0} \phi_{0} \color{magenta}{u_{4}} - \psi_{0} \phi_{1} \color{yellow}{u_{5}} + \psi_{1} \phi_{0} \color{black}{u_{6}} - \psi_{1} \phi_{1} \color{gray}{u_{7}}\\\psi_{0} \phi_{0} \color{brown}{u_{8}} - \psi_{0} \phi_{1} \color{lime}{u_{9}} + \psi_{1} \phi_{0} \color{olive}{u_{10}} - \psi_{1} \phi_{1} \color{orange}{u_{11}}\\\psi_{0} \phi_{0} \color{pink}{u_{12}} - \psi_{0} \phi_{1} \color{purple}{u_{13}} + \psi_{1} \phi_{0} \color{teal}{u_{14}} - \psi_{1} \phi_{1} \color{violet}{u_{15}}\end{matrix}\right]$$

$$\displaystyle \ket{11}\rightarrow\left[\begin{matrix}- \psi_{0} \phi_{0} \color{green}{u_{1}} + \psi_{0} \phi_{1} \color{red}{u_{0}} - \psi_{1} \phi_{0} \color{cyan}{u_{3}} + \psi_{1} \phi_{1} \color{blue}{u_{2}}\\- \psi_{0} \phi_{0} \color{yellow}{u_{5}} + \psi_{0} \phi_{1} \color{magenta}{u_{4}} - \psi_{1} \phi_{0} \color{gray}{u_{7}} + \psi_{1} \phi_{1} \color{black}{u_{6}}\\- \psi_{0} \phi_{0} \color{lime}{u_{9}} + \psi_{0} \phi_{1} \color{brown}{u_{8}} - \psi_{1} \phi_{0} \color{orange}{u_{11}} + \psi_{1} \phi_{1} \color{olive}{u_{10}}\\- \psi_{0} \phi_{0} \color{purple}{u_{13}} + \psi_{0} \phi_{1} \color{pink}{u_{12}} - \psi_{1} \phi_{0} \color{violet}{u_{15}} + \psi_{1} \phi_{1} \color{teal}{u_{14}}\end{matrix}\right]$$

but I lose the property that both parties "keep their qubit".

Answer 1

$\newcommand{\ket}[1]{|#1\rangle}$

This paper: arXiv:quant-ph/0005101 shows how a circuit, closely related to the CNOT teleportation from the question, can be generalized to arbitrary controlled 2-qubit gates.

This circuit again assumes a maximally entangled state ($\ket{\Phi^+}$) shared between the 2 qubits in the middle, where qubit $1$ belongs to $A$ and qubit $2$ belongs to $B$. The dashed vertical lines represent classical communication.

To generalize this circuit to arbitrary controlled 2-qubit gates, the CNOT of the RECEIVER ($B$) is replaced by $U$:

(First entangle qubits $q_1$ and $q_2$ then perform the teleportation. Gates cut by the red line are realized via measurements and classical communication.)

In this generalization we assume $U$ to be an arbitrary controlled gate:

$$\displaystyle U(\ket{\psi}\otimes\ket{\phi})=\left[\begin{matrix}1 & 0 & 0 & 0\\0 & 1 & 0 & 0\\0 & 0 & \color{red}{u_{0}} & \color{green}{u_{1}}\\0 & 0 & \color{blue}{u_{2}} & \color{cyan}{u_{3}}\end{matrix}\right]\cdot\left[\begin{matrix}\psi_{0} \phi_{0}\\\psi_{0} \phi_{1}\\\psi_{1} \phi_{0}\\\psi_{1} \phi_{1}\end{matrix}\right]=\left[\begin{matrix}\psi_{0} \phi_{0}\\\psi_{0} \phi_{1}\\\psi_{1} \phi_{0} \color{red}{u_{0}} + \psi_{1} \phi_{1} \color{green}{u_{1}}\\\psi_{1} \phi_{0} \color{blue}{u_{2}} + \psi_{1} \phi_{1} \color{cyan}{u_{3}}\end{matrix}\right]$$

---

Remark:

I didn't really look into it, but, to me, this circuit doesn't seem to work for arbitrary 2-qubit gates, i.e.

$$\displaystyle U(\ket{\psi}\otimes\ket{\phi})=\left[\begin{matrix}\color{red}{u_{0}} & \color{green}{u_{1}} & \color{blue}{u_{2}} & \color{cyan}{u_{3}}\\\color{magenta}{u_{4}} & \color{yellow}{u_{5}} & \color{black}{u_{6}} & \color{gray}{u_{7}}\\\color{brown}{u_{8}} & \color{lime}{u_{9}} & \color{olive}{u_{10}} & \color{orange}{u_{11}}\\\color{pink}{u_{12}} & \color{purple}{u_{13}} & \color{teal}{u_{14}} & \color{violet}{u_{15}}\end{matrix}\right]\cdot\left[\begin{matrix}\psi_{0} \phi_{0}\\\psi_{0} \phi_{1}\\\psi_{1} \phi_{0}\\\psi_{1} \phi_{1}\end{matrix}\right]=\left[\begin{matrix}\psi_{0} \phi_{0} \color{red}{u_{0}} + \psi_{0} \phi_{1} \color{green}{u_{1}} + \psi_{1} \phi_{0} \color{blue}{u_{2}} + \psi_{1} \phi_{1} \color{cyan}{u_{3}}\\\psi_{0} \phi_{0} \color{magenta}{u_{4}} + \psi_{0} \phi_{1} \color{yellow}{u_{5}} + \psi_{1} \phi_{0} \color{black}{u_{6}} + \psi_{1} \phi_{1} \color{gray}{u_{7}}\\\psi_{0} \phi_{0} \color{brown}{u_{8}} + \psi_{0} \phi_{1} \color{lime}{u_{9}} + \psi_{1} \phi_{0} \color{olive}{u_{10}} + \psi_{1} \phi_{1} \color{orange}{u_{11}}\\\psi_{0} \phi_{0} \color{pink}{u_{12}} + \psi_{0} \phi_{1} \color{purple}{u_{13}} + \psi_{1} \phi_{0} \color{teal}{u_{14}} + \psi_{1} \phi_{1} \color{violet}{u_{15}}\end{matrix}\right]$$

Here are the resulting states of the circuit with arbitrary $U$ and without compensations (gates cut by the dashed red line) written as $\ket{q_1q_2}\rightarrow\ket{\psi\phi}$:

$$\displaystyle \ket{00}\rightarrow\left[\begin{matrix}\psi_{0} \phi_{0} \color{red}{u_{0}} + \psi_{0} \phi_{0} \color{brown}{u_{8}} + \psi_{0} \phi_{1} \color{green}{u_{1}} + \psi_{0} \phi_{1} \color{lime}{u_{9}}\\\psi_{0} \phi_{0} \color{pink}{u_{12}} + \psi_{0} \phi_{0} \color{magenta}{u_{4}} + \psi_{0} \phi_{1} \color{purple}{u_{13}} + \psi_{0} \phi_{1} \color{yellow}{u_{5}}\\\psi_{1} \phi_{0} \color{olive}{u_{10}} + \psi_{1} \phi_{0} \color{blue}{u_{2}} + \psi_{1} \phi_{1} \color{orange}{u_{11}} + \psi_{1} \phi_{1} \color{cyan}{u_{3}}\\\psi_{1} \phi_{0} \color{teal}{u_{14}} + \psi_{1} \phi_{0} \color{black}{u_{6}} + \psi_{1} \phi_{1} \color{violet}{u_{15}} + \psi_{1} \phi_{1} \color{gray}{u_{7}}\end{matrix}\right]$$

$$\displaystyle \ket{01}\rightarrow\left[\begin{matrix}\psi_{0} \phi_{0} \color{red}{u_{0}} - \psi_{0} \phi_{0} \color{brown}{u_{8}} + \psi_{0} \phi_{1} \color{green}{u_{1}} - \psi_{0} \phi_{1} \color{lime}{u_{9}}\\- \psi_{0} \phi_{0} \color{pink}{u_{12}} + \psi_{0} \phi_{0} \color{magenta}{u_{4}} - \psi_{0} \phi_{1} \color{purple}{u_{13}} + \psi_{0} \phi_{1} \color{yellow}{u_{5}}\\- \psi_{1} \phi_{0} \color{olive}{u_{10}} + \psi_{1} \phi_{0} \color{blue}{u_{2}} - \psi_{1} \phi_{1} \color{orange}{u_{11}} + \psi_{1} \phi_{1} \color{cyan}{u_{3}}\\- \psi_{1} \phi_{0} \color{teal}{u_{14}} + \psi_{1} \phi_{0} \color{black}{u_{6}} - \psi_{1} \phi_{1} \color{violet}{u_{15}} + \psi_{1} \phi_{1} \color{gray}{u_{7}}\end{matrix}\right]$$

$$\displaystyle \ket{10}\rightarrow\left[\begin{matrix}\psi_{0} \phi_{0} \color{olive}{u_{10}} + \psi_{0} \phi_{0} \color{blue}{u_{2}} + \psi_{0} \phi_{1} \color{orange}{u_{11}} + \psi_{0} \phi_{1} \color{cyan}{u_{3}}\\\psi_{0} \phi_{0} \color{teal}{u_{14}} + \psi_{0} \phi_{0} \color{black}{u_{6}} + \psi_{0} \phi_{1} \color{violet}{u_{15}} + \psi_{0} \phi_{1} \color{gray}{u_{7}}\\\psi_{1} \phi_{0} \color{red}{u_{0}} + \psi_{1} \phi_{0} \color{brown}{u_{8}} + \psi_{1} \phi_{1} \color{green}{u_{1}} + \psi_{1} \phi_{1} \color{lime}{u_{9}}\\\psi_{1} \phi_{0} \color{pink}{u_{12}} + \psi_{1} \phi_{0} \color{magenta}{u_{4}} + \psi_{1} \phi_{1} \color{purple}{u_{13}} + \psi_{1} \phi_{1} \color{yellow}{u_{5}}\end{matrix}\right]$$

$$\displaystyle \ket{11}\rightarrow\left[\begin{matrix}- \psi_{0} \phi_{0} \color{olive}{u_{10}} + \psi_{0} \phi_{0} \color{blue}{u_{2}} - \psi_{0} \phi_{1} \color{orange}{u_{11}} + \psi_{0} \phi_{1} \color{cyan}{u_{3}}\\- \psi_{0} \phi_{0} \color{teal}{u_{14}} + \psi_{0} \phi_{0} \color{black}{u_{6}} - \psi_{0} \phi_{1} \color{violet}{u_{15}} + \psi_{0} \phi_{1} \color{gray}{u_{7}}\\\psi_{1} \phi_{0} \color{red}{u_{0}} - \psi_{1} \phi_{0} \color{brown}{u_{8}} + \psi_{1} \phi_{1} \color{green}{u_{1}} - \psi_{1} \phi_{1} \color{lime}{u_{9}}\\- \psi_{1} \phi_{0} \color{pink}{u_{12}} + \psi_{1} \phi_{0} \color{magenta}{u_{4}} - \psi_{1} \phi_{1} \color{purple}{u_{13}} + \psi_{1} \phi_{1} \color{yellow}{u_{5}}\end{matrix}\right]$$

However, the paper (arXiv:quant-ph/0005101) also addresses the issue of arbitrary 2-qubit gates:

General single-bit rotations together with a CNOT gate are sufficient to implement any multi-qubit unitary transformation. This implies that the resource requirements for the implementation of a CNOT gate are a limiting factor in the construction of general unitary transformations in a distributed quantum computer.