Why does the point $(0,0,-1)$ on the bloch sphere correspond to the state $|1\rangle$ and not $-|1\rangle$ or $e^{i \phi}|1\rangle$?

Question

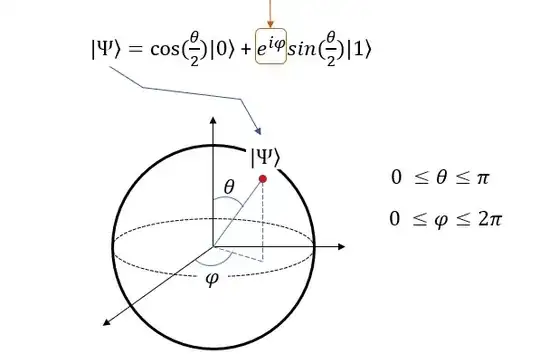
In this representation for points on the $Z$-axis, $\phi$ is not defined. If the point $(0, 0, 1)$ is taken since $\theta$ is $0$ and $\sin(\theta/2)$ is zero, it doesn't matter what $\phi$ is. The point $(0, 0, 1)$ represents state $|0\rangle$.

But for point $(0, 0, -1)$, $\theta$ is $\pi$. $\sin(\pi/2) = 1$ and $\cos(\pi/2) = 0$. So the state is $e^{i \phi}|1\rangle$ where $\phi$ is not defined.

But I saw that point $(0, 0, -1)$ corresponds to state $|1\rangle$. Why? There is an equal chance of it being $-|1\rangle$ or any other state of type $c|1\rangle$ where $c$ is a complex number and $|c| = 1$.

Answer 1

The $e^{i\phi}$ factor you are referring to is called a global phase. You can read more about that here. When you are talking about the state $-|1\rangle$, this $e^{i\pi} = -1$ factor has no physical relevance. Your probability of outcome doesn't change.

For us, states $e^{i\phi} | 1\rangle$ for any value of $\phi$ are equilvalent. It is an artefact of the mathematical framework that we use$^1$, and there is no physical relevance to this global phase. You cannot measure this quantity physically, nor does it have any effect on your outcomes/measurements.

So every point on the Bloch sphere not only corresponds to a state $|\psi\rangle$ but every possible state $e^{i \phi}|\psi\rangle$, where $\phi \in \mathbb{R}$.

---

^{Note: Complex variable $c$ with $|c| = 1$ that you are talking about, is this $e^{i\phi}$ factor.
1: We generally say states are vectors in Hilbert space, however, we actually work with rays in Projective Hilbert space. One state corresponds to a ray where points on this ray are exactly all $e^{i \phi}|\psi\rangle$ states for different values of $\phi$. You can read more about these here.}