Can we express $CX_{2,1}CX_{1,2}$ as single standard 2-qubits gate?

Question

I'd like to know if the above circuit can be synthesised as any single standard 2-qubit gate -- e.g. an Ising gate.

Eventually, other 1-qubit correcting gates.

EDIT: with standard I mean any gate that has practical implication. Especially when this can be directly implemented on hardware.

Answer 1

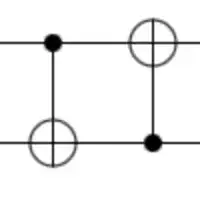
Note that this gate combination is equivalent to a CNOT followed by a SWAP:

In stim this gate is correspondingly called CXSWAP (and its inverse is called SWAPCX):

SWAPCX

A combination SWAP-then-CX gate. This gate is kak-equivalent to the iswap gate, but preserves X/Z noise bias.

Stabilizer Generators:

X_ -> _X
Z_ -> ZZ
_X -> XX
_Z -> Z_

Unitary Matrix (little endian):

[+1  ,     ,     ,     ]
[    ,     ,     , +1  ]
[    , +1  ,     ,     ]
[    ,     , +1  ,     ]

Decomposition (into H, S, CX, M, R):

# The following circuit is equivalent (up to global phase) to `SWAPCX 0 1`
CNOT 0 1
CNOT 1 0

import stim
c = stim.Circuit("CXSWAP 0 1")
c.diagram(type='timeline-svg')

We used CXSWAP gate in the paper "Relaxing Hardware Requirements for Surface Code Circuits using Time-dynamics", to explain iswap-based surface code circuits. A CXSWAP is the same as an iswap gate, up to single qubit rotations before and afterwards, but has the nice property that it doesn't mix the X and Z bases which makes constructions easier to explain and diagram: