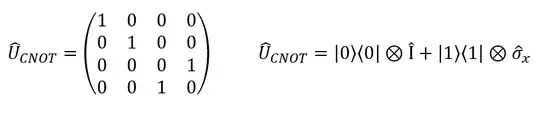How to go from matrix to bra-ket representation of the CNOT?

Question

I have the following definition for CNOT gate form my notes:

I am trying to derive the bracket notation form the matrix version, can someone help me to see where I am going wrong:

$$U ̂_{CNOT} =|00⟩⟨00|+|01⟩⟨01|+|11⟩⟨10|+|10⟩⟨11|$$ $$=?=$$ $$=(|00⟩⟨00|+|01⟩⟨01|) +(|1⟩⟨0| ) $$ $$=(|0⟩⟨0||00⟩⟨00|+|0⟩⟨0||01⟩⟨01|+|0⟩⟨0||10⟩⟨10|+|0⟩⟨0||11⟩⟨11|) +(|1⟩⟨1||0⟩⟨1|+|1⟩⟨1||1⟩⟨0| ) $$ $$=|0⟩⟨0|⊗(|00⟩⟨00|+|01⟩⟨01|+|10⟩⟨10|+|11⟩⟨11|) +|1⟩⟨1|⊗(|0⟩⟨1|+|1⟩⟨0| ) $$ $$U_{CNOT} =|0⟩⟨0|⊗I+|1⟩⟨1|⊗σ_x$$

The above would be make sense if:

$$|1⟩⟨1|⊗(|0⟩⟨1|+|1⟩⟨0| )=(|1⟩⟨1||0⟩⟨1|+|1⟩⟨1||1⟩⟨0| )=?=(|1⟩|0⟩⟨1|⟨1|+|1⟩|1⟩⟨0|⟨1| ) $$

But why would this be correct but not: $$|1⟩⟨1|⊗(|0⟩⟨1|+|1⟩⟨0| )=(|1⟩⟨1||0⟩⟨1|+|1⟩⟨1||1⟩⟨0| )=?=(|1⟩(0)⟨1|+|1⟩(1)⟨0| )=|1⟩⟨0| $$

Answer 1

Your attempt at an answer is a bit ropey in a few places. For starters, you need to be consistent about the number of qubits you have in places. This is a two-qubit operation, so your kets will always have a total of 2 qubits, and your bras will always have a total of two qubits. On your third line, one term only has 1 qubit in each. On your fourth line, you suddenly have 3 qubits in some terms.

I suspect what might help you is putting a subscript on your bras/kets to keep track of which one each term applies to. By that, I mean that you should write out something like $|01\rangle\langle 10|$ as either $|0\rangle_A|1\rangle_B\langle 1|_A\langle 0|_B$ or, just $|0\rangle\langle 1|_A\otimes |1\rangle\langle 0|_B$. These things are all equivalent.

So, for manipulating the description of cNOT, you start from $$ |00\rangle\langle 00|+|01\rangle\langle 01|+|11\rangle\langle 10|+|10\rangle\langle 11|, $$ which I'm instead going to write as $$ |0\rangle\langle 0|_A\otimes |0\rangle\langle 0|_B+ |0\rangle\langle 0|_A\otimes |1\rangle\langle 1|_B+ |1\rangle\langle 1|_A\otimes |1\rangle\langle 0|_B+ |1\rangle\langle 1|_A\otimes |0\rangle\langle 1|_B $$ Now we can group some terms $$ |0\rangle\langle 0|_A\otimes (|0\rangle\langle 0|_B+|1\rangle\langle 1|_B)+ |1\rangle\langle 1|_A\otimes (|1\rangle\langle 0|_B+|0\rangle\langle 1|_B). $$ Now you can recognise the two terms in brackets as $I$ and $X$ respectively.