4

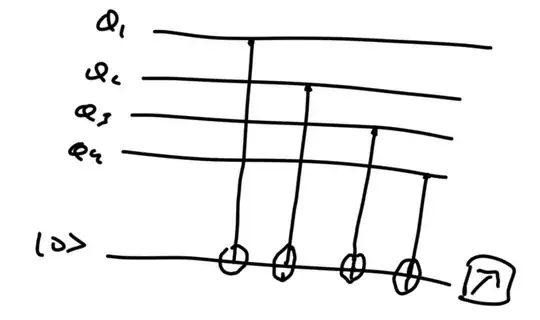
So I am working with a variational quantum algorithm and I realised that it would be very beneficial if I could create an ansatz where all the states in the superposition have same numbers of 1s. For example, if I am working with a 5 qubit system, I want the ansatz to look like this :

$$|{\psi \rangle = a_0| 10001\rangle + a_1|10010 \rangle + a_2|10100 \rangle + a_3| 11000\rangle + a_4|01001 \rangle + a_5| 01010\rangle + a_6| 01100\rangle + a_7|00101 \rangle + a_8| 00110\rangle + a_9|00011 \rangle }$$

for number of ones = 2 or

$$| \psi \rangle = a_0|10000 \rangle + a_1|01000 \rangle + a_2| 00100\rangle + a_3| 00010\rangle + a_4| 00001 \rangle$$
for number of ones = 1

(These two are different ansatz and will be used for different runs of the VQA)

Is there a way to create this kind of ansatz for different total number of qubits and number of ones?

Some extra background on my problem :

  • This kind of selection would help me access more information about the Hamiltonian I am dealing with. I am not sure about the number of parameters, they're definitely less for 2/3 qubits but higher dimensions might require a lot more parameters.

  • I am trying to solve a tight binding hamiltonian and if I create the ansatz in this way, I can find the lowest eigenvalue of all the subsystems and not only th lowest eigenvalue of the whole fock space.

Cheshta Joshi
  • 159
  • 4

2 Answers2

3

Yes, there is, and you are correct that it can be very useful for Ansatz construction - the algorithm name you are looking for is Dicke state preparation. Dicke states are a uniform superposition of Hamming weight k. As @Tristan Nemoz has linked to, this paper describes a Dicke state preparation algorithm, which was subsequently improved in this paper and this paper.

I worked on two papers which then used these short depth Dicke state constructions to create quantum telecloning circuits: paper1 and paper2 - these papers have linked code implementations.

Elijah Pelofske
  • 687
  • 3
  • 10
0

Following similar answer by @DaftWullie and @Tristan Nemoz on How to perform a state density modification for a single targeted state only? , I believe this can be done as follows:

enter image description here

Measuring the last bit will enforce the parity of the number of $|1\rangle$'s in $q_1q_2q_3q_4...$. If the measurement result is $|1\rangle$, discard and start over. If the measurement result is $|0\rangle$, then the remaining superposition must contain an even number of control $|1\rangle$'s in $q_1q_2q_3q_4...$ as desired.

There should exist more complex variations of this parity check to distinguish, for example, $0,1,2,3 \mod{4}$, i.e. the exact number of $|1\rangle$'s in $q_1q_2q_3q_4$...

James
  • 491
  • 2
  • 11
  • 4
    Don't forget the Hadamard gates at the beginning! :D And I don't think this approach works well here. Each time you're checking a parity, there's a $\frac12$ probability of starting over. Thus, the probability of success of this approach seems to be $\frac{1}{2^{\log n}}=\frac1n$. A direct projection isn't good either: if $h$ is the hamming weight, the projection will succeed with probability $\frac{\binom{n}{h}}{2^n}$.

    Fortunately, we do know an efficient deterministic construction for the case with $h=1$. For the other cases, see the discussion in the question I've linked in the comments.

     – Tristan Nemoz Jul 19 '23 at 17:51